March 24th 2024
A physicist wants to change your perspective about our place in the universe
In Waves in an Impossible Sea, Matt Strassler explains how human life is intimately connected to the larger cosmos
January 8th 2024
Why some people don’t trust science – and how to change their minds
Published: December 29, 2023 11.42am GMT
Author
- Laurence D. Hurst Professor of Evolutionary Genetics at The Milner Centre for Evolution, University of Bath
Disclosure statement
Laurence D. Hurst receives funding from The Evolution Education Trust. He is affiliated with The Genetics Society. Dr Cristina Fonseca also contributed to this article as well as to some of the research mentioned that was funded by The Genetics Society.
Partners
University of Bath provides funding as a member of The Conversation UK.
The Conversation UK receives funding from these organisations
 We believe in the free flow of information
We believe in the free flow of information
Republish our articles for free, online or in print, under Creative Commons licence.
During the pandemic, a third of people in the UK reported that their trust in science had increased, we recently discovered. But 7% said that it had decreased. Why is there such variety of responses?
For many years, it was thought that the main reason some people reject science was a simple deficit of knowledge and a mooted fear of the unknown. Consistent with this, many surveys reported that attitudes to science are more positive among those people who know more of the textbook science.
But if that were indeed the core problem, the remedy would be simple: inform people about the facts. This strategy, which dominated science communication through much of the later part of the 20th century, has, however, failed at multiple levels.
In controlled experiments, giving people scientific information was found not to change attitudes. And in the UK, scientific messaging over genetically modified technologies has even backfired.
We believe in experts. We believe knowledge must inform decisions
The failure of the information led strategy may be down to people discounting or avoiding information if it contradicts their beliefs – also known as confirmation bias. However, a second problem is that some trust neither the message nor the messenger. This means that a distrust in science isn’t necessarily just down to a deficit of knowledge, but a deficit of trust.
With this in mind, many research teams including ours decided to find out why some people do and some people don’t trust science. One strong predictor for people distrusting science during the pandemic stood out: being distrusting of science in the first place.
Understanding distrust
Recent evidence has revealed that people who reject or distrust science are not especially well informed about it, but more importantly, they typically believe that they do understand the science.
This result has, over the past five years, been found over and over in studies investigating attitudes to a plethora of scientific issues, including vaccines and GM foods. It also holds, we discovered, even when no specific technology is asked about. However, they may not apply to certain politicised sciences, such as climate change.
Recent work also found that overconfident people who dislike science tend to have a misguided belief that theirs is the common viewpoint and hence that many others agree with them.

Other evidence suggests that some of those who reject science also gain psychological satisfaction by framing their alternative explanations in a manner that can’t be disproven. Such is often the nature of conspiracy theories – be it microchips in vaccines or COVID being caused by 5G radiation.
But the whole point of science is to examine and test theories that can be proven wrong – theories scientists call falsifiable. Conspiracy theorists, on the other hand, often reject information that doesn’t align with their preferred explanation by, as a last resort, questioning instead the motives of the messenger.
When a person who trusts the scientific method debates with someone who doesn’t, they are essentially playing by different rules of engagement. This means it is hard to convince sceptics that they might be wrong.
Finding solutions
So what we can one do with this new understanding of attitudes to science?
The messenger is every bit as important as the message. Our work confirms many prior surveys showing that politicians, for example, aren’t trusted to communicate science, whereas university professors are. This should be kept in mind.
The fact that some people hold negative attitudes reinforced by a misguided belief that many others agree with them suggests a further potential strategy: tell people what the consensus position is. The advertising industry got there first. Statements such as “eight out ten cat owners say their pet prefers this brand of cat food” are popular.
A recent meta-analysis of 43 studies investigating this strategy (these were “randomised control trials” – the gold standard in scientific testing) found support for this approach to alter belief in scientific facts. In specifying the consensus position, it implicitly clarifies what is misinformation or unsupported ideas, meaning it would also address the problem that half of people don’t know what is true owing to circulation of conflicting evidence.
A complementary approach is to prepare people for the possibility of misinformation. Misinformation spreads fast and, unfortunately, each attempt to debunk it acts to bring the misinformation more into view. Scientists call this the “continued influence effect”. Genies never get put back into bottles. Better is to anticipate objections, or inoculate people against the strategies used to promote misinformation. This is called “prebunking”, as opposed to debunking.
Different strategies may be needed in different contexts, though. Whether the science in question is established with a consensus among experts, such as climate change, or cutting edge new research into the unknown, such as for a completely new virus, matters. For the latter, explaining what we know, what we don’t know and what we are doing – and emphasising that results are provisional – is a good way to go.
By emphasising uncertainty in fast changing fields we can prebunk the objection that a sender of a message cannot be trusted as they said one thing one day and something else later.
But no strategy is likely to be 100% effective. We found that even with widely debated PCR tests for COVID, 30% of the public said they hadn’t heard of PCR.
A common quandary for much science communication may in fact be that it appeals to those already engaged with science. Which may be why you read this.
That said, the new science of communication suggests it is certainly worth trying to reach out to those who are disengaged.
December 29th 2023
How Analyzing Cosmic Nothing Might Explain Everything
Huge empty areas of the universe called voids could help solve the greatest mysteries in the cosmos

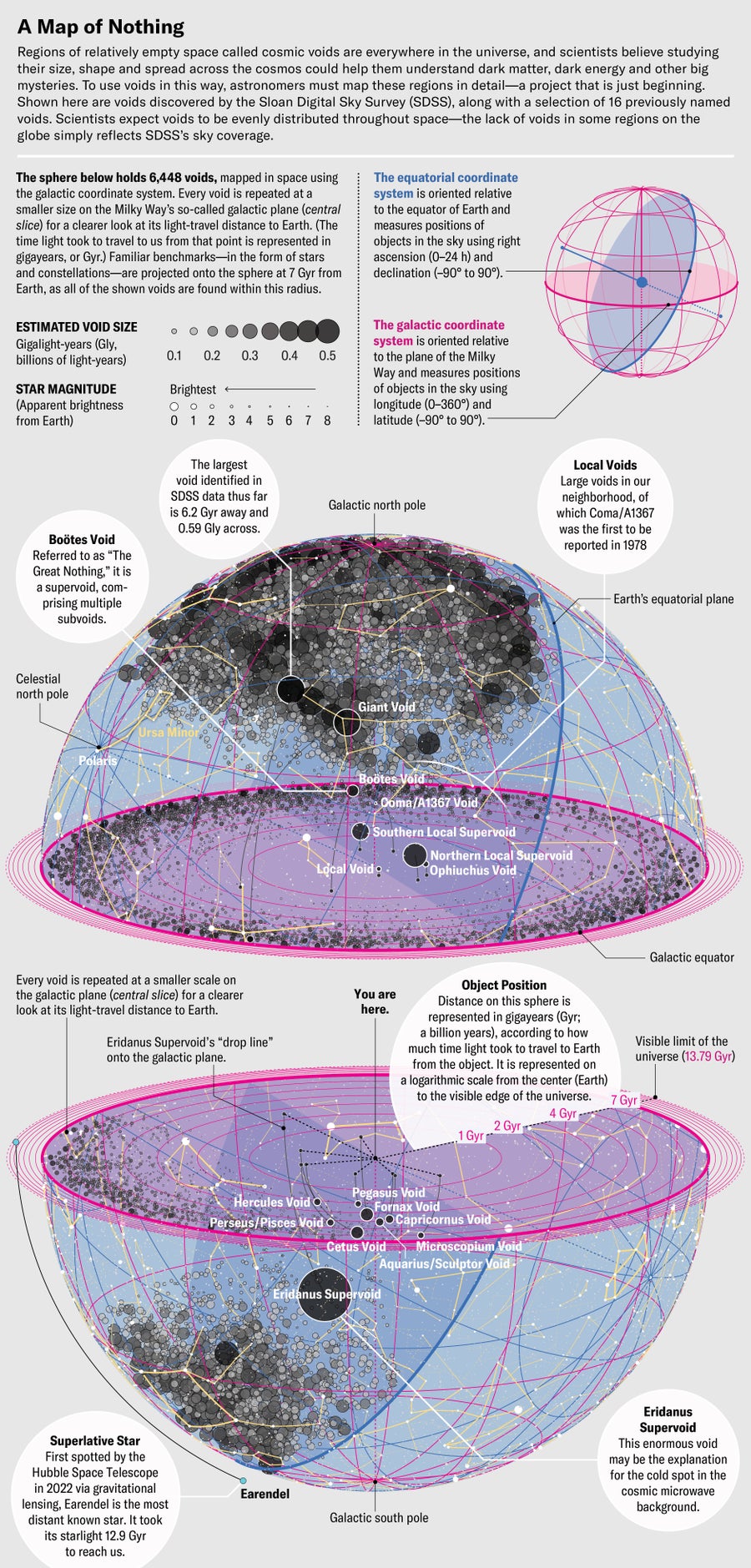
Computational astrophysicist Alice Pisani put on a virtual-reality headset and stared out into the void—or rather a void, one of many large, empty spaces that pepper the cosmos. “It was absolutely amazing,” Pisani recalls. At first, hovering in the air in front of her was a jumble of shining dots, each representing a galaxy. When Pisani walked into the jumble, she found herself inside a large swath of nothing with a shell of galaxies surrounding it. The image wasn’t just a guess at what a cosmic void might look like; it was Pisani’s own data made manifest. “I was completely surprised,” she says. “It was just so cool.”
The visualization, made in 2022, was a special project by Bonny Yue Wang, then a computer science undergraduate at the Cooper Union for the Advancement of Science and Art in New York City. Pisani teaches a course there in cosmology—the structure and evolution of the universe. Wang had been aiming to use Pisani’s data on voids, which can stretch from tens to hundreds of millions of light-years across, to create an augmented-reality view of these surprising features of the cosmos.
The project would have been impossible a decade ago, when Pisani was starting out in the field. Scientists have known since the 1980s that these fields of nothing exist, but inadequate observational data and insufficient computing power kept them from being the focus of serious research. Lately, though, the field has made tremendous progress, and Pisani has been helping to bring it into the scientific mainstream. Within just a few years, she and an increasing number of scientists are convinced, the study of the universe’s empty spaces could offer important clues to help solve the mysteries of dark matter, dark energy and the nature of the enigmatic subatomic particles called neutrinos. Voids have even shown that Einstein’s general theory of relativity probably operates the same way at very large scales as it does locally—something that has never been confirmed. “Now is the right moment to use voids” for cosmology, says David Spergel, former chair of astrophysics at Princeton University and current president of the Simons Foundation. Benjamin Wandelt of the Lagrange Institute in Paris echoes the sentiment: “Voids have really taken off. They’re becoming kind of a hot topic.”
The discovery of cosmic voids in the late 1970s to mid-1980s came as something of a shock to astronomers, who were startled to learn that the universe didn’t look the way they’d always thought. They knew that stars were gathered into galaxies and that galaxies often clumped together into clusters of dozens or even hundreds. But if you zoomed out far enough, they figured, this clumpiness would even out: at the largest scales the cosmos would look homogeneous. It wasn’t just an assumption. The so-called cosmic microwave background (CMB)—electromagnetic radiation emitted about 380,000 years after the big bang—is extremely homogeneous, reflecting smoothness in the distribution of matter when it was created. And even though that was nearly 14 billion years ago, the modern universe should presumably reflect that structure.
But we can’t tell whether that’s the case just by looking up. The night sky appears two-dimensional even through a telescope. To confirm the presumption of homogeneity, astronomers needed to know not only how galaxies are distributed across the sky but how they’re distributed in the third dimension of space—depth. So they needed to measure the distance from Earth to many galaxies near and far to figure out what’s in the foreground, what’s in the background and what’s in the middle. In 1978 Laird A. Thompson of the University of Illinois Urbana-Champaign and Stephen A. Gregory of the University of New Mexico did just that and discovered the first hints of cosmic voids, shaking the presumption that the universe was smooth. In 1981 Harvard University’s Robert Kirshner and four of his colleagues discovered a huge void, about 400 million light-years across, in the direction of the constellation Boötes. It was so big and so empty that “if the Milky Way had been in the center of the Boötes void, we wouldn’t have known there were other galaxies [in the universe] until the 1960s,” as Gregory Scott Aldering, now at Lawrence Berkeley National Laboratory, once put it.
In 1986 Margaret J. Geller, John Huchra and Valérie de Lapparent, all then at Harvard, confirmed that the voids Thompson, Kirshner and their colleagues had found were no flukes. The team had painstakingly surveyed the distance to many hundreds of galaxies spread out over a wide swath of sky and found that voids appeared to be everywhere. “It was so exciting,” says de Lapparent, now director of research at the Institut d’Astrophysique de Paris (IAP). She had been a graduate student at the time and was spending a year working with Geller, who was trying to understand the large-scale structure of the universe. A cross section of the local cosmos that astronomers had put together earlier showed hints of a filamentary structure consisting of regions either overdense or underdense with galaxies. “Margaret had this impression that this was just an observing bias,” de Lapparent says, “but we had to check. We wanted to look farther out.” They used a relatively small telescope on Mount Hopkins in Arizona. “I learned to observe on that telescope,” de Lapparent recalls. “I was on my own after a night of training, which was so exciting.” When she was done, she, Geller and Huchra made a map of the galaxies’ locations. “It was amazing,” she says. “We had these big, circular voids and these sharp walls full of galaxies.”
Related Stories
- Vitamin D Hope and Hype, Cosmic Voids and Preventing DepressionLaura Helmuth
- The Most Shocking Discovery in Astrophysics Is 25 Years OldRichard Panek
- A Possible Crisis in the Cosmos Could Lead to a New Understanding of the UniverseMichael D. Lemonick
- Why Is the Sky Dark Even Though the Universe Is Full of Stars?Brian Jackson & The Conversation US
“All of these features,” the researchers wrote in their paper, entitled “A Slice of the Universe,” “pose serious challenges for current models for the formation of large-scale structure.” As later, deeper surveys would confirm, galaxies and clusters of galaxies are themselves concentrated into a gigantic web of concentrated regions of matter connected by streaming filaments, with gargantuan voids in between. In other words, the cosmos today vaguely resembles Swiss cheese, whereas the CMB looks more like cream cheese.
The question, then, was: What forces made the universe evolve from cream cheese into Swiss cheese? One factor was almost certainly dark matter, the invisible mass whose existence had in the 1980s only recently been accepted by most astrophysicists, despite years of tantalizing evidence from observers such as Vera Rubin and Fritz Zwicky. It was more massive than ordinary, visible matter by a factor of six or so. That would have made the gravitational pull of slightly overdense regions in the early universe stronger than anyone had guessed. Stars and galaxies would have formed preferentially in these areas of high density, leaving low-density regions largely empty.
Most observers and theorists continued to explore what would come to be known as the “cosmic web,” but very few concentrated on voids. It wasn’t for lack of interest; the problem was that there wasn’t much to look at. Voids were important not because of what they contained but because their very existence, their shapes and sizes and distances from one another, had to be the result of the same forces that gave structure to the universe. To use voids to understand how those forces worked, astrophysicists needed to include many examples in statistical analyses of voids’ average size and shape and separation, yet too few had been found to draw useful conclusions from them. It was analogous to the situation with exoplanets in the 1990s: the first few discovered were proof that planets did indeed orbit stars beyond the sun, but it wasn’t until the Kepler space telescope began raking them in by the thousands after its 2009 launch that planetary scientists could say anything meaningful about how many and what kinds of planets populated the Milky Way.
Another issue with studying voids was raised in 1995 by Barbara Ryden of the Ohio State University and Adrian L. Melott of the University of Kansas. Galaxy surveys, they pointed out, are conducted in “redshift space,” not actual space. To understand what they meant, consider that as the universe expands, light waves are stretched from their original wavelengths and colors into longer, redder wavelengths. The farther away something is from an observer, the more its light is stretched. The James Webb Space Telescope was designed to be sensitive to infrared light in part so it can see the very earliest galaxies, whose light has been stretched all the way out of the visible spectrum—it’s redder than red. And the CMB, the most distant light we can detect, has been stretched so much that we now perceive it in the form of microwaves. “Measuring the physical distances to galaxies is difficult,” Ryden and Melott wrote in a paper in the Astrophysical Journal. “It’s much easier to measure redshifts.” But, they noted, redshifts can distort the actual distances to galaxies that enclose a void and thus give a misleading idea of their size and shape. The problem, explains Nico Hamaus of the Ludwig Maximilian University of Munich, is that as a void expands, “the near side is coming toward us, and the far side is streaming away.” That differential subtracts from the redshift on the near side and adds to it on the far side, making the void look artificially elongated.
Despite the difficulties, astrophysicists began to feel more equipped to tackle voids by the late 2000s. Projects such as the Sloan Digital Sky Survey had probed much more deeply into the cosmos than the map made by Geller, Huchra and de Lapparent and confirmed that voids were everywhere you looked. Independent observations by two teams of astrophysicists, meanwhile, had revealed the existence of dark energy, a kind of negative gravity that was forcing the universe to expand faster and faster rather than slowing down from the mutual gravitational attraction of trillions of galaxies. Voids seemed to offer astronomers a promising way of studying what might be driving dark energy.
These developments caught Wandelt’s eye. His specialty has always been trying to understand how the large-scale structure of the modern universe came to be. One of the aspects of voids that he found attractive, he says, was that “these underdense regions are much quieter in some ways, more amenable to modeling” than the clusters and filaments that separate them. Galaxies and gases are crashing into each other in nonlinear and complicated interactions, Wandelt says. There’s “a chaos” that erases the information about their formation. Further complicating things, the gravitational attraction between galaxies is strong enough on smaller scales that it counteracts the general expansion of the universe—and even counteracts the extra oomph of dark energy. Andromeda, for example, the nearest large galaxy to our own, is actually drawing closer to the Milky Way; in four billion years or so, they’ll merge. Voids, in contrast, “are dominated by dark energy,” Wandelt says. “The biggest ones are actually expanding faster than the rest of the universe.” That makes them ideal laboratories for getting a handle on this still puzzling force.
Sign Up for Our Daily Newsletter
Email AddressBy giving us your email, you are agreeing to receive the Today In Science newsletter and to our Terms of Use and Privacy Policy.
And it’s not just an understanding of dark energy that could emerge from this line of study; voids could also cast light (so to speak) on the nature of dark matter. Although voids have much less dark matter in them than the clusters and filaments of the cosmic web do, there’s still some. And unlike the chaotic web, with its swirling hot gases and colliding galaxies, the voids are calm enough that the particles astrophysicists think make up dark matter might be detectable. They wouldn’t show up directly, because they neither absorb nor emit light. But the particles should occasionally collide, resulting in tiny bursts of gamma rays. They would also probably decay eventually, releasing gamma rays in that process as well. A sufficiently sensitive gamma-ray telescope in space would theoretically be able to detect their collective signal. Nicolao Fornengo of the University of Turin in Italy, co-author of a preprint study laying out this rationale, says that “if dark matter produces [gamma rays], the signal should be in there.”

Voids could even help to nail down the nature of neutrinos—elementary particles, once thought to be massless, that pervade the universe while barely interacting with ordinary matter. (If you sent a beam of neutrinos through a slab of lead one light-year, or nearly six trillion miles, thick, about half of them would sail through it effortlessly.) Physicists have confirmed that the three known types of neutrinos do have masses, but they aren’t sure why or exactly what those masses are.
Voids could help them find the answer, says Elena Massara, a postdoctoral researcher at the Waterloo Center for Astrophysics at the University of Waterloo in Canada. They’re places that have a lack of both luminous matter and dark matter, she explains, “but they’re full of neutrinos, which are almost uniformly distributed” through the universe, including in voids.That’s because neutrinos zip through the cosmos at nearly the speed of light, which means they don’t clump together under their mutual gravity—or under the gravity of the dark matter concentrations that act as the scaffolding for the cosmic web. Although voids always contain a lot of neutrinos, the particles are only passing through—those that fly out are constantly replenished by more neutrinos streaming in. And their combined gravity can make the voids grow more slowly over time than they would otherwise. The rate of growth—determined through comparison of the average size of voids in the early universe to those in the modern universe—can reveal how much mass neutrinos actually have.
Void science has changed a lot since Pisani started studying it as a graduate student working with Wandelt. He offered two or three suggestions for a dissertation topic, she recalls, and one of them was cosmic voids. “I felt that they were the riskiest choice,” she says, “because there were very few data at the time. But they were also incredibly challenging,” which she found exciting. The data Pisani and others needed to analyze the voids, however—that is, to test their real-world properties against computer models incorporating dark matter, dark energy, neutrinos and the formation of large-scale structure in the universe—were simply not available. “When I started my Ph.D. thesis,” Pisani says, “we knew of fewer than 300 voids, something like that. Today we have on the order of 6,000 or more.”
That’s huge, but it’s still not enough for the comprehensive statistical analysis necessary for voids to be used for serious cosmology—with one exception. In 2020 Hamaus, Pisani, Wandelt and several of their colleagues published an analysis showing that general relativity behaves at least approximately the same way on very large scales as it seems to do in the local universe. Voids can be used to test this question because astrophysicists think they result from the way dark matter clusters in the universe: the dark matter pulls in ordinary matter, creating the cosmic web and leaving empty spaces behind. But what if general relativity, our best theory of gravity, breaks down somehow over very large distances? Few scientists expect that to be the case, but it has been suggested as a means to explain away the existence of dark matter.
By looking at the thickness of the walls of matter surrounding voids, however, Hamaus and his colleagues determined that Einstein’s theory is safe to rely on. To understand why, imagine a void as “a circle whose radius increases with the expansion of the universe,” Wandelt says. As the circle grows, it pushes against the boundaries of galaxies and clusters at its perimeter. Over time these structures aggregate, thickening the “wall” that defines the void’s edge. Dark energy and neutrinos affect the thickness as well, but because they are smoothly distributed both inside and outside the voids, they have a much smaller effect overall.
Scientists plan to use voids to learn even more about the universe soon because they expect to rapidly multiply the number of known voids in their catalog. “In the next five or 10 years,” Pisani says, “we’re going to have hundreds of thousands. It’s one of those fields where numbers really make a difference.” So, Spergel says, do advances in machine learning, which will make it far easier to analyze void properties.
These exploding numbers won’t be coming from projects explicitly designed to search for voids. They will arrive, as they did with the Sloan Digital Sky Survey, as a by-product of more general surveys. The European Space Agency’s Euclid mission, for example, which launched in July 2023, will create a 3-D map of the cosmic web with unprecedented breadth and depth. NASA’s Nancy Grace Roman Space Telescope will begin its own survey in 2026, looking in infrared light. And in 2024 the ground-based Vera C. Rubin Observatory will launch a 10-year study of cosmic structure, among other things. Combined, these projects should increase the inventory of known voids by two orders of magnitude.
“I remember one of the first talks I gave on void cosmology, at a conference in Italy,” Pisani says. “At the end the audience had no questions.” She wasn’t sure at the time whether the reason was skepticism or simply that the topic was so new to her listeners that they couldn’t think of anything to ask. In retrospect, she thinks it was a little of both. “Initially, I think the problem was just convincing people that this was reasonable science to look into,” she says.
That’s much less of an issue now. For example, Pisani points out, the Euclid voids group has about 100 scientists in it. “I have to say that Alice was one of the fearless pioneers of this field,” Wandelt notes about his former Ph.D. student. When they started writing the first papers on void science, he recalls, some of the leading figures in astrophysics “expressed severe doubt that you could do anything cosmologically interesting with voids.” The biggest confirmation that they were wrong, he says, is that some of those same people are now enthusiastic.
Pisani is perhaps the ideal representative for this fast-emerging field. She approaches the topic with absolute scientific rigor but also with infectious enthusiasm. Whenever she talks about voids, she lights up, speaking rapidly, jumping to her feet to draw diagrams on a whiteboard, and fielding questions (of which there are now many) with ease and confidence. She emphasizes that void science won’t answer all of astrophysicists’ big questions about the universe by itself. But it could do something even more valuable in a way: test ideas about dark matter, dark energy, neutrinos and the growth of cosmic structure independently of the other strategies scientists use. If the results match, great. If not, astrophysicists will have to reconcile their differences to find out what’s actually going on in the cosmos.
“I find the idea attractive and even somewhat poetic,” Wandelt says, “that looking into these areas where there’s nothing might yield information about some of the outstanding mysteries of the universe.”
Michael D. Lemonick is a freelance writer, as well as former chief opinion editor at Scientific American and a former senior science writer at Time. His most recent book is The Perpetual Now: A Story of Amnesia, Memory and Love (Doubleday, 2017). Lemonick also teaches science journalism at Princeton University.
This article was originally published with the title “Cosmic Nothing” in Scientific American Magazine Vol. 330 No. 1 (January 2024), p. 20
doi:10.1038/scientificamerican0124-20
Popular Stories
Public Health January 1, 2024How Much Vitamin D Do You Need to Stay Healthy?
Most people naturally have good vitamin D levels. Overhyped claims that the compound helps to fight diseases from cancer to depression aren’t borne out by recent research
Christie AschwandenWater January 1, 2024Why Are Alaska’s Rivers Turning Orange?
Streams in Alaska are turning orange with iron and sulfuric acid. Scientists are trying to figure out why
Alec LuhnGenetics January 1, 2024Sperm Cell Powerhouses Contain Almost No DNA
Scientists discover why fathers usually don’t pass on their mitochondria’s genome
Sneha KhedkarPharmaceuticals December 21, 2023How Two Pharmacists Figured Out That Decongestants Don’t Work
A loophole in FDA processes means older drugs like the ones in oral decongestants weren’t properly tested. Here’s how we learned the most popular one doesn’t work
Randy HattonEpidemiology December 19, 2023The Real Story Behind ‘White Lung Pneumonia’
Separate outbreaks of pneumonia in children have cropped up in the U.S., China and Europe. Public health experts say the uptick in cases is not caused by a novel pathogen
Today’s Silicon Valley billionaires grew up reading classic American science fiction. Now they’re trying to make it come true, embodying a dangerous political outlook
Charles Stross
Expand Your World with Science
Learn and share the most exciting discoveries, innovations and ideas shaping our world today.SubscribeSign up for our newslettersSee the latest storiesRead the latest issue

June 20th 2023
Airbus experiments with more control for the autopilot

By Shiona McCallum & Ashleigh Swan
Technology reporters
It’s difficult not to be a bit overwhelmed by the Airbus campus in Toulouse.
It is a huge site and the workplace for 28,000 staff, plus hundreds of visitors eager to see the planes being built.
The enormous Beluga cargo plane is parked at a loading dock, ready to transport vehicles and satellites around the world.
Close to where we conduct our interviews is the hangar where the supersonic passenger jet Concorde was developed.
This site is also home to much Airbus research and development, including the recently finished Project Dragonfly – an experiment to extend the ability of the autopilot.
Over the past 50 years automation in aviation has transformed the role of the pilot. These days pilots have a lot more assistance from tech in the cockpit.
Project Dragonfly, conducted on an Airbus A350-1000, extended the plane’s autonomy even further.
The project focused on three areas: improved automatic landing, taxi assistance and automated emergency diversion.

Perhaps the last of those is the most dramatic.
Malcolm Ridley, Chief Test Pilot of Airbus’s commercial aircraft, reassured us that the risk of being involved in an air accident is “vanishingly small”.
However, aircraft and crew need to be ready for any scenario, so Project Dragonfly tested an automatic emergency descent system.
The idea is this technology will take over if the pilots need to focus on heavy decision-making or if they were to become incapacitated.
Under its own control, the plane can descend and land, while recognising other aircraft, weather and terrain.
The system also allows the plane to speak to air traffic control over the radio with a synthetic voice created through the use of artificial intelligence.
It is a lot for the plane’s systems to take on.
One of the challenges was teaching the system to understand all of the information and create a solution, says Miguel Mendes Dias, Automated Emergency Operations Designer.
“The aircraft needs to, on its own, recover all the information. So it needs to listen for the airport messages from air traffic control.
“Then it needs to choose the most suitable airport for diversion,” he said.
Project Dragonfly performed two successful emergency descents.
During the test flights, French air traffic controllers fully understood the situation and the aircraft landed safely.
“It was really an amazing feat,” says Mr Mendes.

Thankfully, almost all landings are much less dramatic, and Project Dragonfly looked at the more usual kind as well.
Most big airports have technology which guides the aircraft on to the runway, called Precision Approach.
But not every airport in the world has that tech, so Airbus has been looking at a different way to land.
Project Dragonfly explored using different sensors to help an aircraft make an automated landing.
It included using a combination of normal cameras, infrared and radar technology.
The team also gathered data from around the world, so all sorts of weather conditions could be modelled.
As well as giving the plane more information, the extra sensors give the pilot extra clarity, when monitoring the landing.
For example, infrared cameras are useful in cloudy conditions, as the closer you get to objects the more of its heat an infrared sensor can pick up.
The tech “will make the pilot comfortable in the fact that he’s really aligned and on the good path to go to the runway,” says Nuria Torres Mataboch, a computer vision engineer on the Dragonfly project.

Project Dragonfly also looked at taxiing. Although this might seem like a basic task, it can be the most challenging part of the job, especially at the world’s busiest airports.
In this case, the pilot was in control of the aircraft.
The technology provided the crew with audio alerts. So when the aircraft came across obstacles it issued an alert. It also advised pilots on speed and showed them the way to the runaway.
“We wanted something that would assist and reduce the pilots’ workloads during the taxi phase,” said Mr Ridley.
What do pilots make of such developments? Some do not want the technology pushed too far.
“I don’t know if any pilot is particularly comfortable with the computer being the sole arbiter of whether or not a flight successfully lands,” said Tony Lucas, president of the Australian and International Pilots Association.

- Can Amsterdam make the circular economy work?
- The ‘exploding’ demand for giant heat pumps
- The chip maker that became an AI superpower
- Why car parks are the hottest space in solar power
- Protein’s power is being uncovered and unleashed

In addition, he is not convinced that self-flying planes will be able to deal with complex scenarios that come up.
“Automation can’t replace the decision making of two well-trained and rested pilots on the flight deck,” he said from his base at Sydney airport.
Mr Lucas used the example of the Boeing 737 Max, where an automated system led to two fatal crashes in 2018 and 2019.
Airbus is quick to point out that further automation will only be introduced when safe and that the objective is not to remove pilots from the cockpit.
But could passenger planes be pilot-free one day?
“Fully automated aircraft would only ever occur if that was clearly and certainly the safe way to go to protect our passengers and crew,” says Mr Ridley.
June 18th 2023
Clean Energy
Scientists Made An Artificial “Cloud” That Pulls Electricity From Air
The secret? Tiny holes.
May 24, 2023

Derek Lovley/Ella Maru Studio
Taking a hint from the magician’s playbook, scientists have devised a way to pull electricity from thin air. A new study out today suggests a method in which any material can offer a steady supply of electricity from the humidity in the air.
All that’s required? A pair of electrodes and a special material engineered to have teeny tiny holes that are less than 100 nanometers in diameter. That’s less than a thousandth of the width of a human hair.
Here’s how it works: The itty-bitty holes allow water molecules to pass through and generate electricity from the buildup of charge carried by the water molecules, according to a new paper published in the journal Advanced Materials.

The process essentially mimics how clouds make the electricity that they release in lightning bolts.
Because humidity lingers in the air perpetually, this electricity harvester could run at any time of day regardless of weather conditions — unlike somewhat unreliable renewable energy technologies such as wind and solar.
“The technology may lead to truly ‘ubiquitous powering’ to electronics,” senior study author Jun Yao, an electrical engineer at the University of Massachusetts Amherst, tells Inverse.
Man-made “clouds”
The recent discovery relies on the fact that the air is chock-full of electricity: Clouds contain a build-up of electric charge. However, it’s tough to capture and use electricity from these bolts.
Instead of trying to wrangle power from nature, Yao and his colleagues realized they could recreate it. The researchers previously created a device that uses a bacteria-derived protein to spark electricity from moisture in the air. But they realized afterward that many materials can get the job done, as long as they’re made with tiny enough holes. According to the new study, this type of energy-harvesting device — which the study authors have dubbed “Air-gen”, referring to the ability to pluck electricity from the air — can be made of “a broad range of inorganic, organic, and biological materials.”
“The initial discovery was really a serendipitous one,” says Yao, “so the current work really followed our initial intuition and lead to the discovery of the Air-gen effect working with literally all kinds of materials.”

Water molecules can travel around 100 nanometers in the air before bumping into each other. When water moves through a thin material that’s filled with these precisely sized holes, the charge tends to build up in the upper part of the material where they enter. Since fewer molecules reach the lower layer, this creates a charge imbalance that’s similar to the phenomenon in a cloud — essentially creating a battery that runs on humidity, which apparently isn’t just useful for making hair frizzy. Electrodes on both sides of the material then carry the electricity to whatever needs powering.
And since these materials are so thin, they can be stacked by the thousands and even generate multiple kilowatts of energy. In the future, Yao envisions everything from small-scale Air-gen devices that can power wearables to those that can offer enough juice for an entire household.
Before any of that can happen, though, Yao says his team needs to figure out how to collect electricity over a larger surface area and how best to stack the sheets vertically to increase the device’s power without taking up additional space. Still, he’s excited about the technology’s future potential. “My dream is that one day we can get clean electricity literally anywhere, anytime by using Air-gen technology,” he says.
more like this

Elon Musk’s Neuralink Brain Implant Approved for Human Trials in the US — Is It Safe?ScienceSummer 2023 Will Likely Break Heat Records — Here’s What To ExpectScienceThis One Metric Is More Important Than Temperature To Know If It’s Safe OutsideLEARN SOMETHING NEW EVERY DAY
Subscribe for free to Inverse’s award-winning daily newsletter!
By subscribing to this BDG newsletter, you agree to our Terms of Service and Privacy Policy
Related Tags
Space Science
Shocking Threads of Gas Could Transform Our Understanding of a Supermassive Black Hole
“I was actually stunned when I saw these.”
June 2, 2023

Credit: Farhad Yusef-Zadeh
Astrophysicists have stumbled upon a strange sight in the center of our galaxy: hundreds of horizontal threads of hot gas hanging out near Sagittarius A*, the Milky Way’s central supermassive black hole that’s located roughly 26,000 light-years away from Earth.
These one-dimensional filaments lie parallel to the galactic plane that surrounds the black hole, according to a new study published in The Astrophysical Journal Letters.
In the 1980s, Northwestern University astrophysicist Farhad Yusef-Zadeh discovered similar filaments arranged vertically, meaning they were aligned with the galaxy’s magnetic field. These measured up to 150 light-years tall and were likely made of high-energy electrons. Last year, his team revealed they had found nearly 1,000 of these vertical filaments, which showed up in pairs and clusters.

But when parsing through data from the MeerKAT radio telescope in South Africa, Yusef-Zadeh and his colleagues encountered a shocking revelation.
“It was a surprise to suddenly find a new population of structures that seem to be pointing in the direction of the black hole,” Yusef-Zadeh said in a press release. “I was actually stunned when I saw these. We had to do a lot of work to establish that we weren’t fooling ourselves.”
The newly discovered threads measure just 5 to 10 light-years long, sit on just one side of the black hole, and seem to point to Sagittarius A*. They may be about 6 million years old, the team estimates and could have formed when a jet erupted from Sagittarius A* and stretched surrounding gas into these odd threads.
This revelation, along with other newer discoveries, wouldn’t have been possible without recent advances in radio astronomy technology, according to Yusef-Zadeh. He and his colleagues relied on a technique that allowed them to remove the background and smooth out noise from MeerKAT images, offering a clear view of the filaments.
“The new MeerKAT observations have been a game changer,” he said. “The advancement of technology and dedicated observing time have given us new information. It’s really a technical achievement from radio astronomers.”
All in all, these new findings from Yusef-Zadeh’s team could teach us more about the mysterious black hole and its inner workings. “By studying them, we could learn more about the black hole’s spin and accretion disk orientation,” he said. “It is satisfying when one finds order in a middle of a chaotic field of the nucleus of our galaxy.”
June 13th 2023
Data Compression Drives the Internet. Here’s How It Works.
One student’s desire to get out of a final exam led to the ubiquitous algorithm that shrinks data without sacrificing information.
Read Later


May 31, 2023
Abstractions blogcomputer sciencecomputerscryptographyexplainersinformation theoryAll topics

Introduction
With more than 9 billion gigabytes of information traveling the internet every day, researchers are constantly looking for new ways to compress data into smaller packages. Cutting-edge techniques focus on lossy approaches, which achieve compression by intentionally “losing” information from a transmission. Google, for instance, recently unveiled a lossy strategy where the sending computer drops details from an image and the receiving computer uses artificial intelligence to guess the missing parts. Even Netflix uses a lossy approach, downgrading video quality whenever the company detects that a user is watching on a low-resolution device.
Very little research, by contrast, is currently being pursued on lossless strategies, where transmissions are made smaller, but no substance is sacrificed. The reason? Lossless approaches are already remarkably efficient. They power everything from the PNG image standard to the ubiquitous software utility PKZip. And it’s all because of a graduate student who was simply looking for a way out of a tough final exam.
Seventy years ago, a Massachusetts Institute of Technology professor named Robert Fano offered the students in his information theory class a choice: Take a traditional final exam, or improve a leading algorithm for data compression. Fano may or may not have informed his students that he was an author of that existing algorithm, or that he’d been hunting for an improvement for years. What we do know is that Fano offered his students the following challenge.
Consider a message made up of letters, numbers and punctuation. A straightforward way to encode such a message would be to assign each character a unique binary number. For instance, a computer might represent the letter A as 01000001 and an exclamation point as 00100001. This results in codes that are easy to parse — every eight digits, or bits, correspond to one unique character — but horribly inefficient, because the same number of binary digits is used for both common and uncommon entries. A better approach would be something like Morse code, where the frequent letter E is represented by just a single dot, whereas the less common Q requires the longer and more laborious dash-dash-dot-dash.

Abstractions navigates promising ideas in science and mathematics. Journey with us and join the conversation.
See all Abstractions blog
Yet Morse code is inefficient, too. Sure, some codes are short and others are long. But because code lengths vary, messages in Morse code cannot be understood unless they include brief periods of silence between each character transmission. Indeed, without those costly pauses, recipients would have no way to distinguish the Morse message dash dot-dash-dot dot-dot dash dot (“trite”) from dash dot-dash-dot dot-dot-dash dot (“true”).
Fano had solved this part of the problem. He realized that he could use codes of varying lengths without needing costly spaces, as long as he never used the same pattern of digits as both a complete code and the start of another code. For instance, if the letter S was so common in a particular message that Fano assigned it the extremely short code 01, then no other letter in that message would be encoded with anything that started 01; codes like 010, 011 or 0101 would all be forbidden. As a result, the coded message could be read left to right, without any ambiguity. For example, with the letter S assigned 01, the letter A assigned 000, the letter M assigned 001, and the letter L assigned 1, suddenly the message 0100100011 can be immediately translated into the word “small” even though L is represented by one digit, S by two digits, and the other letters by three each.
To actually determine the codes, Fano built binary trees, placing each necessary letter at the end of a visual branch. Each letter’s code was then defined by the path from top to bottom. If the path branched to the left, Fano added a 0; right branches got a 1. The tree structure made it easy for Fano to avoid those undesirable overlaps: Once Fano placed a letter in the tree, that branch would end, meaning no future code could begin the same way.
Share this article
Newsletter
Get Quanta Magazine delivered to your inbox

Introduction
To decide which letters would go where, Fano could have exhaustively tested every possible pattern for maximum efficiency, but that would have been impractical. So instead he developed an approximation: For every message, he would organize the relevant letters by frequency and then assign letters to branches so that the letters on the left in any given branch pair were used in the message roughly the same number of times as the letters on the right. In this way, frequently used characters would end up on shorter, less dense branches. A small number of high-frequency letters would always balance out some larger number of lower-frequency ones.

Introduction
The result was remarkably effective compression. But it was only an approximation; a better compression strategy had to exist. So Fano challenged his students to find it.
Fano had built his trees from the top down, maintaining as much symmetry as possible between paired branches. His student David Huffman flipped the process on its head, building the same types of trees but from the bottom up. Huffman’s insight was that, whatever else happens, in an efficient code the two least common characters should have the two longest codes. So Huffman identified the two least common characters, grouped them together as a branching pair, and then repeated the process, this time looking for the two least common entries from among the remaining characters and the pair he had just built.
Consider a message where the Fano approach falters. In “schoolroom,” O appears four times, and S/C/H/L/R/M each appear once. Fano’s balancing approach starts by assigning the O and one other letter to the left branch, with the five total uses of those letters balancing out the five appearances of the remaining letters. The resulting message requires 27 bits.
Huffman, by contrast, starts with two of the uncommon letters — say, R and M — and groups them together, treating the pair like a single letter.

Introduction
His updated frequency chart then offers him four choices: the O that appears four times, the new combined RM node that is functionally used twice, and the single letters S, C, H and L. Huffman again picks the two least common options, matching (say) H with L.

Introduction
The chart updates again: O still has a weight of 4, RM and HL now each have a weight of 2, and the letters S and C stand alone. Huffman continues from there, in each step grouping the two least frequent options and then updating both the tree and the frequency chart.



Introduction
Ultimately, “schoolroom” becomes 11101111110000110110000101, shaving one bit off the Fano top-down approach.

Introduction
One bit may not sound like much, but even small savings grow enormously when scaled by billions of gigabytes.
Related:
- How Shannon Entropy Imposes Fundamental Limits on Communication
- Researchers Defeat Randomness to Create Ideal Code
- The Scientist Who Developed a New Way to Understand Communication
- How Do You Prove a Secret?
Indeed, Huffman’s approach has turned out to be so powerful that, today, nearly every lossless compression strategy uses the Huffman insight in whole or in part. Need PKZip to compress a Word document? The first step involves yet another clever strategy for identifying repetition and thereby compressing message size, but the second step is to take the resulting compressed message and run it through the Huffman process.
Not bad for a project originally motivated by a graduate student’s desire to skip a final exam.
Correction: June 1, 2023
An earlier version of the story implied that the JPEG image compression standard is lossless. While the lossless Huffman algorithm is a part of the JPEG process, overall the standard is lossy.
The Quanta Newsletter
Get highlights of the most important news delivered to your email inboxEmail
May 11th 2023
Ancient Androids: Even Before Electricity, Robots Freaked People Out
Automata—those magical simulations of living beings—have long enchanted the people who see them up close.
- Lisa Hix
Read when you’ve got time to spare.
Advertisement

More from Collectors Weekly
- Fun Delivered: World’s Foremost Experts on Whoopee Cushions and Silly Putty Tell All
- Mudlarking the Thames for Relics of Long-Ago Londoners
- How a Small-Town Navy Vet Created Rock’s Most Iconic Surrealist Posters
Advertisement

The term “robot” was coined in the 1920s, so it’s tempting to think of the robot as a relatively recent phenomenon, less than 100 years old. After all, how could we bring metal men to life before we could harness electricity and program computers? But the truth is, robots are thousands of years old.
The first records of automata, or self-operating machines that give the illusion of being alive, go back to ancient Greece and China. While it’s true none of these ancient androids could pass the Turing Test, neither could early 20th-century robots—it’s only in the last 60 years that scientists began to develop “artificial brains.” But during the European Renaissance, machinists built life-size, doll-like automata that could write, draw, or play music, producing the startling illusion of humanity. By the late 19th century, these magical machines had reached their golden age, with a wide variety of automata available in high-end Parisian department stores, sold as parlor amusements for the upper middle class.
One of the largest publicly held collections of automata, including 150 such Victorian proto-robots, lives at the Morris Museum in Morristown, New Jersey, as part of the Murtogh D. Guinness Collection, which also features 750 mechanical musical instruments, from music boxes and reproducing pianos to large orchestrions and band organs.

Top: Swiss mechanician Henri Maillardet, an apprentice of Pierre Jaquet-Droz, built this boy robot, the Draughtsman-Writer, circa 1800. His automaton could write four poems and draw four sketches. Above: A drawing by Maillardet’s automaton. (Via the Franklin Institute of Philadelphia)
“Murtogh Guinness was one of the elders of the Guinness brewing family based in Dublin, Ireland,” says Jere Ryder, an automata expert and the conservator of the Guinness Collection. “Guinness traveled extensively throughout the world with his parents, and they had homes around the globe. But just after World War II, he decided he loved New York City best—with its opera, ballet, Broadway shows, and antiques—so he established a permanent residence there. That’s when he rediscovered mechanical music and automata and started to collect them with a passion.” Guinness died at age 89 in January 2002, and a year later, his collection was awarded to the Morris Museum.
Ryder’s connection to Murtogh Guinness goes way back. His parents, Hughes and Frances Ryder, were collectors and members of the Musical Box Society International. In the late 1950s, Guinness, then in his 40s, had learned of their music-box collection. When Jere and his brother, Stephen, first met the Guinness heir, they were toddlers.
“Guinness—who never drove himself anywhere—had to call a taxi to bring him all the way out to New Jersey from New York City,” Ryder says, remembering that first meeting. “He came knocking on our door in the evening. I was about 2 years old, and my brother, Steve, was just a year older. That was the night Guinness first met my father and my mother, and they struck up a lifelong friendship. He and my dad both had a passion for collecting these things. Of course, our family was not in the same league, collecting-wise. Mr. Guinness had the wherewithal to take it to a whole different level.” Given his early exposure, it’s no wonder Ryder would go on to apprentice with automata makers in Switzerland, repair and sell automata for a living, and write extensively on the subject with his brother.

Pierrot writes his love, Columbine, under the light of an oil lamp in this 1875 scene by Parisian automata manufacturer Vichy. At the time, artisans building automata would have been working under oil or gas lamps. (Via the Murtogh D. Guinness Collection at the Morris Museum)
In May 2018, the Morris Museum hosted its second-ever AutomataCon, which brought together 300 makers, collectors, and fans of all things automata. The convention corresponded with an annual exhibition of modern-day kinetic art. Of course, a rotating exhibition of half-a-dozen pieces from the Guinness Collection are on display at the museum year-round, and live demonstrations of selected machines take place at 2 p.m., Tuesdays through Sundays [at the time of this writing in 2018].
“In keeping with Murtogh Guinness’ wishes, we provide regular demonstrations of selected instruments and automata,” says Michele Marinelli, the curator of the collection. “These are moving pieces. They need to be seen and heard.”
The demonstrations always draw a crowd of gawkers. “When people today first see these things operate or hear them play, they’re just mesmerized,” Ryder says. “If people are in the next room and you turn one on, it’s like a magnet. They ask, ‘When were these made?’ We tell them, ‘Before electric lights.’
“These were the state-of-the-art entertainment devices of their day,” Ryder continues. “Back then, people didn’t have iPods, or even radios. The phonograph hadn’t been invented. Think of that. Now, place yourself in that period and imagine you’re watching or hearing this technology. At the Morris Museum, we try to remove people from the cacophony of today’s electronics to help them imagine the impact of these machines.”

Jacquemarts, or “jacks-of-the-clock,” also known as bellstrikers, were among the earliest clockwork automata. This jacquemart is on St. Peter’s Collegiate Church in Leuven, Belgium. Photo via WikiCommons
Automata—those magical simulations of living beings—have long enchanted the people who see them up close. Ancient humans first captured their own likenesses with paintings, sculptures, and dolls. Then, they made dolls that could move and, eventually, puppets.
“Man’s fascination with replicating human or living creatures’ characteristics is an ancient thing,” Ryder says. “Back in the earliest times, the makers of carved dolls started to use articulated limbs, with joints at the shoulders, knees, and hips in order to pose the dolls, before they had a way to mechanize the figures. It’s all an outgrowth of this human desire to see life replicated in a realistic manner.”
If you’ve ever watched the original “Clash of the Titans” and assumed Bubo the metallic owl was a preposterous 1981 Cold War anachronism, you might be surprised to learn that metal or wooden fowl were the stuff of legend for ancient Greeks, as much as Medusa and Perseus were. Around the globe, stories from mythology, religious scripture, and apocryphal historical texts describe wondrous moving statues, incredible androids with leather organs, and mobile metallic animals—particularly in temples and royal courts—but it’s hard to sort fact from fiction.

In the early 16th century, Leonardo da Vinci sketched a mechanical dove (inset), a concept made into a mechanical toy in the 19th century (main image). (From Leonardo’s Lost Robots)
For example, the Greek engineer Daedalus was said to have built human statues that walked by the magical power of “ quicksilver” around 520 BCE, but it’s more likely the statues appeared to move through the power of his clever engineering. In “ The Seventh Olympian,” 5th-century BCE Greek poet Pindar described the island of Rhodes as “The animated figures stand / Adorning every public street / And seem to breathe in stone, or / move their marble feet.”
Nor were automata a uniquely Western preoccupation. Around 500 BCE, King Shu in China is said to have made a flying wood-and-bamboo magpie (like Lu Ban’s bird a hundred years later, it was probably similar to a kite) and a wooden horse driven by springs, long before spring technology was perfected.
The Greek mathematician Archytas of Tarentum is credited with creating a wooden dove around 350 BCE that could flap its wings and fly 200 meters. It’s likely the device was connected to a cable and powered by a pulley and counterweight, but some have speculated it was animated by an internal system of compressed air or an early steam engine.

A display of two outflow water clocks, or clepsydrae, from the Ancient Agora Museum in Athens. The top is an original from the late 5th century BC. The bottom is a reconstruction of a clay original. (Via WikiCommons)
Besides the obvious connection to dolls and puppetry, automata were long connected to clock-making. In ancient times, that meant water-driven mechanisms, similar to fountains. The earliest timepiece, the clepsydra or water clock—developed as early as 1700s BCE and found in Babylonia, Egypt, and China—used the flow of water in or out of a bowl to measure time.
According to Mark E. Rosheim in his book, Robot Evolution, Greek inventor Ctesibius, also spelled Ktesibios, is thought of as the founder of modern-day automata. Around 280 BCE, and he started building water clocks that had moving figures, like an owl, and whose waterworks forced air into pipes to blow whistles. Essentially, he built the first cuckoo clock. Ctesibius also amused people with a hydraulic device that caused a fake blackbird to sing, as well as mechanical figures that appeared to move and drink.
The Morris Museum’s Jere Ryder explains that because none of these ancient devices survived, it’s hard to know how they worked. “The speaking heads or the talking animals might not have had articulated limbs,” he explains. “They were more like sculptures, which might have had water-driven pneumatic instruments to create guttural sounds of an animal. This could be accomplished by opening a sluice gate or tap so water could turn a wheel, which then turned cams on a cog that worked a bellows. Or perhaps a person, hidden out of sight, would talk through a tube. You’d be walking by this bronze or stone statue, and all of a sudden, realistic sounds would be emanating from it. The experience would have been magical, almost wizard-like. That’s why automata were sometimes regarded as witchcraft.”

A 2007 mechanical model based on the ancient Greek Antikythera machine. (Photo by Mogi Vicentini, WikiCommons)
According to historian Joseph Needham in his epic study of ancient Chinese engineering, Science and Civilisation in China, in the 3rd century BCE, Chinese engineers and mathematicians like Chang Hêng, who worked for the royal court, were focused on how to animate full-scale puppet shows. Han emperor Chhin Shih Huang Ti, as known as Qin Shi Huang, was said to have had a device that featured a band of a dozen 3-foot-tall bronze men that played real music, but it still required two unseen puppeteers to operate, one blowing into a tube for the sound and another pulling a rope for the movement.
Back in Greece, Ctesibius’ student, Philo (or Philon) of Byzantium, was a pioneer who advanced from pneumatics to steam-driven automata and other devices around 220 BCE, writing a book called Mechanike syntaxis . Only part of Philo’s work has survived. Unfortunately, the true depth of Greek and Roman engineering and the extent to which they employed steam power are unknown, as many records were destroyed in the centuries of wars after the fall of the Roman Empire.
The first real evidence of the ancient Greeks’ mechanical abilities was the discovery of the Antikythera mechanism, dated between 205 and 60 BCE. This clock mechanism, which used 30 bronze gears and cams, is thought of as the first computer and may have been employed to operate automata.

This sketch, based on Hero of Alexandra’s writings describing water- and weight-driven bird automata, appeared in Sigvard Strandh’s 1989 book, The History of the Machine.
The earliest full-length book of Greek robots that’s survived is On Automatic Theaters, on Pneumatics, and on Mechanics, written circa 85 CE, by the inventor Hero (or Heron) of Alexandria. In his treatise, Hero describes mechanical singing birds, robot servants that pour wine, and full-scale automated puppet theaters that employed everything from weights and pulleys to water pipes, siphons, and steam-driven wheels. Mostly, the automata executed simple, repetitive motions. Because Romans kept human slaves and servants to do hard labor and menial tasks, apparently no one thought to give robots actual work.
Since Hero’s writings left out certain details and didn’t include drawings, depictions of his machines still require a lot of guesswork, explains Rosheim in Robot Evolution. For example, the Hero automaton known as “Hercules and the Beast” has been drawn showing the legendary hunk shooting a snake with a bow and arrow and, alternately, depicting Hercules pounding a dragon with a club. What we do know is the action depended on water draining into hidden vessels that served as counterweights.

This interpretation of Hero’s “Hercules and the Beast” was drawn in 1598 as an illustration for a translation of On Automatic Theaters. (Via Robot Evolution)
But progress on building robots in the Western World halted as the Roman Empire began to crumble around 117 CE. In the meantime, circa 3rd-7th century CE, according to Needham, the Chinese continued to develop elaborate puppet theaters with myriad figures of musicians, singers, acrobats, animals, and even government officials at work, which would move and make music. They were likely operated by water-driven wheels, and possibly underwater chains, ropes, or paddle wheels.
In the 600s, Chinese engineer Huang Kun, serving under Sui Yang Ti, described an outdoor mechanical puppet theater in the palace courtyards and gardens with 72 finely dressed figures that drifted on barges floating down a channel. To impress his guests, the emperor’s automata would stop to serve them wine. In Science and Civilization in China, Needham quotes Huang’s manual: “At each bend, where one of the emperor’s guests was seated, he was served with wine in the following way. The ‘Wine Boat’ stopped automatically when it reached the seat of a guest, and the cup-bearer stretched out its arm with the full cup. When the guest had drunk, the figure received it back and held it for the second one to fill again with wine. Then immediately the boat proceeded, only to repeat the same at the next stop. All these were performed by machinery set in the water.”

Medieval Chinese engineer Su Song designed this escapement for his famous astronomical clock tower that included jacquemart-type figures to announce the hours. (Via WikiCommons)
The Tu-Yang Tsa Pien ( Miscellaneous Records from Tu-Yang) has this intriguing story of automata in 9th century China: “A guardsman, Han Chih-Ho, who was Japanese by origin … made a wooden cat which could catch rats and birds. This was carried to the emperor, who amused himself by watching it. Later, Han made a framework which was operated by pedals and called the ‘Dragon Exhibition.’ This was several feet in height and beautifully ornamented. At rest there was nothing to be seen, but when it was set in motion, a dragon appeared as large as life with claws, beard, and fangs complete. This was presented to the emperor, and sure enough, the dragon rushed about as if it was flying through clouds and rain; but now the emperor was not amused and fearfully ordered the thing to be taken away.”
Naturally, Han feared for his life. “Han Chih-Ho threw himself upon his knees and apologized for alarming his imperial master, offering to present some smaller examples of his skill. The emperor laughed and inquired about his lesser techniques. So Han took a wooden box several inches square from his pocket, and turned out from it several hundred ‘tiger-flies,’ red in color, which he said was because they had been fed on cinnabar. Then he separated them into five columns to perform a dance. When the music started they all skipped and turned in time with it, making small sounds like the buzzing of flies. When the music stopped they withdrew one after the other into their box as if they had rank. … The emperor, greatly impressed, bestowed silver and silks on him, but as soon as he had left the palace he gave them all away to other people. A year later he disappeared and no one could ever find him again.”

In the 12th century, Isma’il Ibn al-Razzaz al-Jazari designed this water-driven miniature “robot band” that sat in a boat on a lake and played music for royal guests.
Around the same time, circa 800s-830s, the Khalif of Baghdad, Abdullah al-Manum, recruited three brothers known as Banū Mūsā to hunt down the Greek texts on mechanical engineering, including Hero’s On Automatic Theaters, on Pneumatics, and on Mechanics. The brothers wrote The Book of Ingenious Devices, which included both their own inventions, like an automatic flute player, and the ancient concepts they’d collected. The 9th century was something of a golden era of Muslim invention, with alchemists and engineers building impressive automata for Muslim rulers, including snakes, scorpions, and humans, as well as trees with metal birds that sang and flapped their wings. Around the same time, the Byzantine Emperor Constantine VII in Constantinople was said to have a similar tree as well as an imposing rising “ throne of Solomon” guarded by two roaring-lion automata.
By the 11th century, India had automata, too. According to History of Indian Theatre by Manohar Laxman Varadpande, a book on architecture, Samarangana Sutradhara, written by Parmar King Bhoja of Malava, describes miniature wooden automata called “das yantra” that decorated palaces and could dance, play musical instruments, or offer guests betel leaves. Other yantra were put in the service of mythological plays and acted out everything from war-making to love-making. Similarly, small humanoid automata were employed in royal residences and temples in Egypt.
Building on the works of Banū Mūsā, in the 12th century, Muslim polymath Isma’il Ibn al-Razzaz al-Jazari produced The Book of Knowledge of Ingenious Mechanical Devices, with lushly colored illustrations of previously invented devices and his own novel inventions. It describes the mechanics of water clocks with moving figures, robot bands, and tabletop automata. For example, al-Jazari’s Peacock Fountain, designed to aid in royal hand-washing, relied on a series of water vessels and floats. According to Rosheim, the water poured from the jewel-encrusted peacock’s beak into a basin. As the water drained into containers under the basin, float devices triggered little doors where miniature-servant automata appeared in a sequence, the first offering soap, the second a towel. Turning another valve caused the servants to retreat.

A drawing from Isma’il Ibn al-Razzaz al-Jazari’s The Book of Knowledge of Ingenious Mechanical Devices shows his concept for the Peacock Fountain, used for royal hand-washing.
The science of automata is thought to have re-emerged in Europe in the 13th century, thanks to the sketchbooks of the French artist Villard de Honnecourt, which describe several machines and automata such as singing birds and an angel that always turned to face the sun. De Honnecourt may have recorded some of the first jacquemarts, or “jacks-of-the-clocks,” automata activated to blow horns or strike bells on medieval-town clock towers. The Strasbourg Cock, built in France in 1352, features a prime example of the jacquemarts of this era: A rooster, one of 12 figures in rotation on an astronomical clock in the Cathedral of Our Lady of Strasbourg, would raise its head, flap its wings, and crow three times to announce its hour. In China, inventors continued to build more and more impressive water-wheel animated puppet theaters, as well as elaborate jacquemarts on their water clocks. But unfortunately, Joseph Needham explains, most records and examples of these mechanical advancements were destroyed by the conquering Ming Dynasty in 1368.
Besides clocks and puppet theaters, in Medieval and Renaissance Europe, automata were a key piece of aristocratic “ pleasure gardens,” which were the equivalent of modern-day fun houses, filled with slapstick booby traps. In the late 13th century, the Count Robert II of Artois (1250-1302), commissioned the first known pleasure garden at Hesdin in France. Walking through the maze, the Count’s guest would be startled by statues that spat water at them, fun-house mirrors, a device that smacked them in the head, a wooden garden hermit and metallic owl that spoke, other mechanical beasts, a guard automata that gave orders and hit them, a collapsing bridge, and other devices that shot out or dumped water, soot, flour, and feathers.

Hellbrunn Palace in Salzburg, Austria, still features trick fountains hidden in seats once used by guests of Prince-Archbishop Markus Sittikus for outdoor meals. (Via WikiCommons)
By the 16th and 17th centuries, a handful of eccentric gardens with fountain automata popped up around modern-day Italy, Germany, and France, like the Villa d’Este at Tivoli near Rome, which featured elaborate fountains and grottos as well as hydraulic organs and animated birds. Perhaps inspired by Hesdin, the Prince-Archbishop of Salzberg (now in Austria), Markus Sittikus von Hohenems, built a prank-filled “water park” at Hellbrunn Palace in the 1610s with water-powered automata and music, where guests would be startled by statues that squirted water in their faces and chairs that shot water on their butts. In 1750, more than 100 years after Sittikus’ death, a water-driven puppet theater, with more than 200 busy townspeople automata, was installed at the estate.
On a smaller scale than the fountain-filled pleasure gardens were the Gothic table fountains of the 14th and 15th centuries, which were like miniature animated puppet theaters, showpieces thought to have come to Western aristocrats through Byzantine and Islamic trade. Dozens of figures on the fountain would dance, play music, or spout wine or perfumed water. It’s believed that most of these devices were made of precious metal and later melted down. The one surviving example, made around 1320 to 1340 and now housed at the Cleveland Museum of Art, was a gift from the Duke of Burgundy to Abu al-Hamid II, the sultan of the Ottoman Empire.

This Gothic table fountain with small automata, now at the Cleveland Museum of Art, was thought to be a typical showpiece for European aristocrats in the 14th and 15th centuries. Because such animated fountains were made of precious metals, most were melted down. (Via the Cleveland Museum of Art)
Up until the 15th century, automata technology had been hindered by the limitations of hydraulic, pneumatic, and weight- and steam-driven motion. That changed with the introduction of steel-spring clockwork mechanisms. Previously, engineers had experimented with using tightly wound metal springs to drive automata and timepieces, but the rudimentary metalwork meant the mechanism might only work right once before breaking. In the 15th and 16th centuries, technological advances made in the steel-working foundries in Nuremberg and Augsburg, Germany, and in Blois, France, were a major breakthrough.
“It wasn’t until the 1400s that Europeans had the sufficient metal refining and foundry techniques to produce a spring that wouldn’t self-destruct,” Morris Museum’s Jere Ryder says. “As time went on, they refined the process further, and the quality of their materials improved.”
Where metalworking flourished, so did horological, or clock-making, technology. Starting around the 1430s, clockmakers in Europe, particularly in Germany and France, were producing key-wound spring-driven clocks. They continued to develop and improve upon clock mechanics throughout the Renaissance, adding more and more elaborate decorative flourishes. In BBC Four’s “ Mechanical Marvels: Clockwork Dreams,” science history professor Simon Schaffer explains that the time-keeping mechanism, which once needed a tower to contain it, got smaller and smaller until pocket watches could be made with tiny screws and gears that artisans meticulously hand-crafted.

The miniaturization of clockwork eventually led to companies like Bontems in Paris producing small musical automata like this singing-hummingbird box from 1890.Photo by WikiCommons
“Clockmakers were usually the technicians making automata,” the Morris Museum’s Jere Ryder says. “They had the access to the materials; they knew the clockwork mechanisms; they knew the drive systems that would be required. They had all the basic metalworking and metallurgical skills and knowledge at their disposal.”
Unlike the whimsical jacquemarts seen on public clock towers, these robots were strictly for the entertainment of royalty and aristocrats, and were only produced by the most trusted court inventors and artisans. “You have to remember, quality metals were a precious commodity, and you had to have somebody of great importance in your region grant you the access to those materials,” Ryder says. “These metals weren’t available to the masses for fear that they would be used to make arms for insurgents to rise up against the aristocracy. As an inventor, you had to be trustworthy because you were getting a potentially dangerous raw substance in your workshop that you could turn into weapons, and that would be a detriment to your patron.”

A page from Giovanni de Fontana’s sketchbook, The Book of Warfare Devices, from 1420.
Some inventors in the early 15th century were still conceptualizing automata through the older technologies of hand cranks and weights and pulleys. Giovanni (or Johannes) de Fontana produced a book of plans for animated monsters and devils that could spit fire, intended to debunk magicians. But it’s hard to say if Fontana successfully built any of these devices, which seem mechanically impractical and unlikely to work. In the mid-15th century, German mathematician and astronomer Johannes Müller von Königsberg, also known as Regiomontanus, is said to have built an iron mechanical fly and a wing-flapping eagle automata—possibly driven by clockwork—that accompanied the Holy Roman Emperor to the gates of Nuremberg, but there are no records of his designs for such machines.
Leonardo da Vinci’s sketchbooks show a full-size clockwork lion, supposedly a present for King Francois I in the 1510s. Witnesses claimed the mechanical lion, a symbol of Florence, approached the king, opened a “heart cavity” on its side, and revealed a Fleur-de-Lis, the symbol of the French monarchy. Da Vinci’s lion has been lost to history, but a replica was constructed by automata-maker Renato Boaretto for Chateau du Clos Luce, in Amboise, France, in 2009. According to Robot Evolution author Mark E. Rosheim, da Vinci’s notebooks offer hints that he was working on an android, dressed in a suit of arms, using a system of pulleys and cables based on his drawing of human musculature, possibly operated by a manual hand crank, as many of da Vinci’s inventions were. However, it’s unclear if he ever built the android, as the relevant pages of his sketchbook are missing.
The writings of Hero of Alexandria were finally translated from Greek into Latin in the 16th century. French engineer Salomon de Caus studied the work of Hero religiously and replicated the hydraulic-pneumatic singing bird concept. Other inventors relied on new developments in wind-up spring technology. In the service of Holy Roman Emperor Charles V in Spain, Italian clockmaker Juanelo Turriano—also known as Gianello Della Tour of Cremona and Giovanni Torriani—made several miniature clockwork robots to entertain the easily bored emperor, from flying birds to soldiers to musicians.
“In the Renaissance, only royalty and aristocrats would be able to afford automata, which they’d commission to show that they were more powerful than their neighbors,” Ryder says. “There was a lot of one-upmanship going on at that time. The owner of automata could assert he was important because he could command these miniature lifelike pieces with amazing clockwork mechanisms to perform at will, anytime he wanted them to. At that time, that was probably pretty darn impressive.”
Although few clockwork automata from the 16th century have survived, we know that the artisans building these robots for royal entertainment had mastered wind-up technology to the point of re-creating the nuances of human movement and facial expressions, causing an “ uncanny valley” effect. One remarkable surviving automaton from this era lives at the Smithsonian Institute. A 15-inch-tall key-wound clockwork Franciscan monk, built as early as 1560, possibly by Juanelo Turriano for Charles V, is a startling imitation of life. The friar walks in a square path, hitting his chest with his right arm, waving a cross and rosary with his left. He nods and turns his head, rolls his eyes, mouths silent prayers, and occasionally lifts his cross to kiss it.
“Underneath the robes, there’s a full clockwork mechanism,” Ryder says. “So you’d have to wind it up, and then he would move across the table with his little feet underneath the robe moving up and down. He really looks like he’s walking.”
Another surviving early clockwork automaton is a 1610 gilt bronze and silver timepiece in the moving form of the goddess Diana on her chariot. It was built for royalty by some unknown maker in Southern Germany, and is now housed at the Yale University Art Gallery. “The chariot’s being drawn across the table slowly by these undulating panthers in front,” Ryder explains. “There’s a monkey on the chariot moving his arm to eat a pomegranate, which is a sign of hospitality. Diana up top has a bronze bow and arrow loaded under tension, as the whole carriage goes down what would have been a large banquet table. It moves for almost 3 feet and stops, her eyes still scanning from side to side with the tick-tock sound, like she’s deciding who her next victim will be. Then, she launches the bronze arrow, and it flies about 6 to 8 feet. It’s a fabulous automaton.”
In the mid-17th century, German Jesuit scholar Athanasius Kircher—the first to describe the automatic barrel organ operated by pinned cylinders—attempted to build a talking head with moving eyes, lips, and tongue, which may have been voiced by an operator talking through a tube. In his 1650 treatise, Musurgia Universalis, Kircher also detailed a barrel organ with an automaton cuckoo. Nineteen years later, Domenico Martinelli wrote a book on horology suggesting the cuckoo’s call be used to announce the hours. In 1730, the first so-called cuckoo clock was produced in the Black Forest. But these were not the first small German clocks with moving automata and sound to declare the hours: The Met Museum has a musical automata clock made by Velt Langenbucher and Samuel Bidermann in Augsburg more than 100 years earlier.

This musical clock with dancing automata, a spinet, and an organ was made by Velt Langenbucher and Samuel Bidermann circa 1625.Photo by Via The Met Museum
“The Augsburg timepiece has got these commedia dell’arte figures in a rotunda atop it,” Ryder says. “Each one turns as they waltz around, circling each other in what looks like a miniature mirrored home. Below the timepiece, there are two automatic musical instruments that play both independently and together in unison—one is a spinet, which is like a miniature harpsichord, and the other is a flute organ. It’s just an outstanding early Augsburg device that combines mechanical music and automata in the same package.”
The most incredibly intricate, full-sized robots were first built in the 1700s. French inventor Jacques de Vaucanson—an anatomy student who would later develop the predecessor to the Jacquard automatic loom—created a life-size human automaton called the Flute Player in 1737. Living in the Age of Enlightenment, Vaucanson wanted to figure out if human and animal bodies operated like machines. Modeled after a famous Antoine Coysevox sculpture of a shepherd, Vaucanson’s weight-driven android actually blew air from a series of connected pipes, bellows, and valves inside its body through its mouth into a flute. The robot also controlled the sound of the instrument by moving its lips and tongue and pressing its fingers—possibly covered with the leather of real human skin—on the holes, playing with a human level of artistic expression. This stunning machine could play more than 12 distinct tunes.

An illustration of three automata built by Jacques de Vaucanson: the Flute Player, the Duck, and the Drummer. Photo by the Rare Book and Special Collections Division, Library of Congress
Vaucanson followed the Flute Player with another life-size android called the Drummer or the Tambourine Player, which played a pipe and a drum, and a bird automata called the Digesting Duck—unfortunately, all three have been lost to time. His crowd-pleasing duck device could quack, rise up on its legs, flap its wings, move its head, bow its neck, drink, eat, and defecate. Vaucanson, and the French entrepreneurs he later sold them to, took his automata on tour, letting members of the European elite pay a hefty fee to witness this buzzed-about anatomical spectacle. (In the 19th century, magician and clockmaker Jean-Eugène Robert-Houdin claimed he encountered this duck automata and took it apart to discover the consumed grain and pooped-out breadcrumbs were in separate chambers, meaning, as brilliant as the device was, no actual “digesting” was involved.)
“Vaucanson held exhibitions in France and Italy that he would invite royalty to,” Ryder says. “Eventually, high-level aristocrats would be invited in, too. That’s how inventors like Vaucanson got money to help subsidize the next project. Those exhibitions weren’t for the masses because they couldn’t afford to get in.” In “Clockwork Dreams,” professor Simon Schaffer explains that, ironically, these robots spelled doom for the aristocrats who funded them. The notion that humans might just be soulless machines—and therefore, the monarchies didn’t have divine authority to subjugate their peasants—eventually led to uprisings against the European elite, like the French Revolution at the end of the century.

Photographs of Vaucanson’s Digesting Duck, taken in the 19th century.Photo by WikiCommons
According to Crescendo of the Virtuoso: Spectacle, Skill, and Self-Promotion in Paris during the Age of Revolution, by Paul Metzner, Vaucanson’s show-stopping demonstrations were so lucrative that 18th-century showmen, naturally, saw automata as a way to make it big. Mechanicians were commissioned to copy Vaucanson and make automata purely for entertainment, not science: These included flute, harpischord, and dulcimer players; singing birds; wine servers; and more. A French inventor and Catholic abbot named Mical was said to have made “an entire orchestra in which the figures, large as life, played music from morning till evening.”

An American artist’s drawing, which incorrectly guessed how the Digesting Duck worked.Photo by WikiCommons
Because the stage entrepreneurs were trying to make a buck, Metzner writes, some builders found ways to cut corners making figures now considered “quasi-automata” because they only gave the illusion of lifelike action. For example, with musician quasi-automata, the music was generated by an automatic organ in the base, and the figure only made the motions of playing the instrument. Singing birds were popular among aristocratic women, and they operated much the same way. Similarly, many showmen claimed to have automata that could write or draw, when in reality, they were showing a life-size puppet, or a “pseudo-automata,” whose pen was guided by a living person in a hidden compartment, operating a pantograph.
However, in the mid-18th century, German watchmaker Friedrich von Knauss did develop automata that could write and draw. Following in Vaucanson’s footsteps, Knauss first successfully built automata that could play music. Then he developed a machine with a hand that could use a quill to spell out “Huic Domui Deus / Nec metas rerum / Nec tempora ponat” (“May God not impose ends or deadlines on this house”) on a card. He also attempted to build four talking heads and failed. None of Knauss’ automata had full bodies.

A 1783 copper engraving of the Turk, showing the open cabinets and working parts. The inventor Wolfgang von Kempelen was a skilled engraver and may have produced this image himself.Photo by WikiCommons
In 1769, Wolfgang von Kempelen, a mechanician in Austria, created a life-size figure known as the Turk or the Chess Player, which was dressed as the Western stereotype of a man from Turkey. This spring-driven automated figure was positioned behind a large wheeled cabinet with a chess board affixed to the top. In his research, Metzner explains that for more than half a century, the Turk put on shows of what appeared to be an incredible display of artificial intelligence, regularly beating audience members at chess. But in the 1830s, it was revealed a man operating a pantograph had been hiding in the cabinet every time. However, Kempelen did have real engineering talent: He made significant advances in the concept of the steam engine, and he, along with Mical and Christian Gottlieb Kratzenstein, developed speaking machines in the 1770s.
Beside the Digesting Duck, another clockwork-fowl automaton that made a splash was the exquisite Silver Swan, built out of real silver by Belgian roller-skate inventor John Joseph Merlin and London clockmaker and showman James Cox in 1773. Today, you can watch this gorgeous moving artwork at the Bowes Museum in England: When wound up, the life-size swan, “floats” on a stream of twisting glass rods, which rotate to the automatic music. Operating with three separate clockwork mechanisms, the swan very elegantly turns to the left and right and preens. Then, it appears to notice a fish in the “water,” catch it in its beak, and swallow it.
Inspired by Vaucanson’s musicians, Swiss clockmaker Pierre Jaquet-Droz made a clock topped by a flute-playing shepherd figure in the 1760s. Then, he and his assistants, including his adopted son, Jean-Frédéric Leschot, built three mind-bending spring-driven automata between 1768 and 1774—the Scribe, the Musician, and the Draughtsman. The Scribe looks like a life-size doll of three-year-old boy, and is still operational today. The child is sitting on a stool, holding a quill to a mahogany table. Wound up and given a piece of paper, the Scribe, whose mechanism is made up of nearly 6,000 parts and 40 distinct cams—can dip his quill into ink and write any sentence up to 40 characters long. (However, the programming is so time-consuming his sentence was rarely changed.) His eyes follow the writing with focus and intent. The Scribe is, in many ways, a predecessor to the modern computer.
The Musician is a full-size adolescent girl who plays a non-automatic organ by pressing the keys with her finger. She appears to watch her fingers, breathe, and adjust her body as a real organist would. The Draughtsman, like the Scribe, looks like a toddler boy, and is capable of producing four different drawings—a dog, a portrait of Louis XV, a royal couple, and Cupid driving a chariot pulled by a butterfly. He also fidgets in his chair and occasionally blows on his pencil. All three of these original automata can be seen in action today at Musée d’Art et d’Histoire of Neuchâtel, Switzerland.
Jaquet-Droz and his sons toured the royal courts around Europe, China, India, and Japan, demonstrating the three automata to grow their watch-making business. These three blockbusting machines were generally not for sale, although a small number were reproduced for kings. The Jaquet-Droz family, like other watchmakers of the era, offered timepieces and miniature automata incorporated into clocks, watches, snuff boxes, perfume bottles, and jewelry to their moneyed clientele.
“In the mid- to late 1700s, Switzerland became a center of very fine, high-end automata,” Ryder says. “You had Pierre Jaquet-Droz, Henri Maillardet, and others who made these writing, drawing, and music-playing automata, as well as a wide range of pocket watches, musical perfume bottles with animated figures, and wind-up jewelry, like lockets, brooches, and rings with music and automata. Jaquet-Droz took his extraordinary large automata on the road as the showpieces that would draw future customers from the upper echelons of the aristocracy. The large automata caught the attention of the press, and wealthy people would pay to visit someone’s chateau to see them in action. But then Jaquet-Droz could sell his smaller wares to these same individuals.”

The Draughtsman, the Musician, and the Scribe at Musée d’Art et d’Histoire of Neuchâtel.Photo by WikiCommons
As much as it was good business, it was also a risky endeavor to pack up these delicate robots made of thousands of cams and gears, put them in carriages, and drive them thousands of miles. “When Jaquet-Droz went down to Madrid to sell to the king’s court, it took 30 days in transit to get there,” Ryder says. “This was high risk and on speculation, because not much of this stuff was sold before he made that trip. He hoped the king and his courtesans would want most of the wares he was bringing. If he didn’t sell it all, then he’d try zigzagging on his way home to try sell the remainder of it. Jaquet-Droz was extremely successful at doing that.”
Swiss clockmaker Henri Maillardet, an apprentice of Pierre Jaquet-Droz, built his own version of the Scribe called t he Draughtsman-Writer, with the help of Pierre’s sons Henri Louis Jaquet-Droz and Jean-Frédéric Leschot, in 1800. Maillardet’s animated doll, which now lives at the Franklin Institute in Philadelphia, can write four poems and draw four sketches. Henri Maillardet’s brother Jean-David Maillardet—with the assistance of his son, Julien-Auguste, and his brother Jacques-Rodolphe—built an automata clock called the Great Magician featuring a conjurer and a set of nine plaques with predetermined questions. The machine can be seen in action today at the International Clock Museum in La Chaux-de-Fonds, Switzerland: When you place a question in a drawer, the magician moves about before a window opens, revealing the answer. Questions include “A rare thing? (A friend)” and “What is too easily given? (Advice)”.

A 19th-century tea-serving automaton doll compared with a similar disrobed figure, its internal mechanisms revealed.Photo by Tokyo National Science Museum, WikiCommons
Around the same time as Jaquet-Droz’s and Maillardet’s automata advances, engineers in Edo Period Japan were building table-top, tea-serving robots, servant dolls with perhaps a little more labor-saving functionality than European robots, which were meant to astonish. Once set in motion, a 14-inch-tall “ karakuri” powered by a whale-baleen spring moves toward a guest holding a cup of tea with its head bowed. After the cup is lifted, the robot seems to wait patiently for the guest to drink. When the cup is replaced, the doll makes a 180-degree turn and moves in the opposite direction.
In 1790s India, a life-size musical automata of a tiger mauling a white European flat on his back was built for the Tipu Sultan (also spelled Tippu or Tippoo), who hated the British colonizers and, specifically, the East India Company. Tipu’s Tiger is 5-foot-8-inches long, constructed of wood, and contains a playable 18-note pipe organ. When a handle is cranked, the man emits a wail, the tiger seems to growl, and the man’s left arm flails up and down. When the East India Company invaded Tipu’s land in the 1799, the automaton was shipped to England, where, ironically, it became a popular curiosity.

Tipu’s Tiger, a life-size Indian musical automata of a wild cat eating an Englishman, also contains a playable organ.Photo from the Victorian and Albert Museum, via WikiCommons
At the turn of the 19th century, German inventor and showman Johann Nepomuk Maelzel became obsessed with collecting and demonstrating the marvels of automata and mechanical music. First, he developed an automatic organ that replicated the sounds of a 40-member orchestra, which he called a Panharmonicon (later classified as an orchestrion). Then, as Paul Metzner explains in Crescendo of the Virtuoso, Maelzel purchased the pseudo-automaton, the Turk, and built a real automaton trumpet player, a real automaton acrobat, and other androids, including talking dolls that spoke one word each. Later, he bought a Draughtsman-Writer by the Jaquet-Droz family. In the early 19th century, he toured the United States with his automata, making a big impression on famous showman P.T. Barnum.
What do all of these machines have in common? They’re all illusions of some sort, which made them natural fits for the magic shows that were growing in popularity in the 19th century. Jean-Eugène Robert-Houdin—the French magician and inventor Houdini named himself after—built several automata for his 1840s stage shows including a magician, a writer-draftsman, a trapeze acrobat, a singing nightingale, and clowns. Robert-Houdin was also famous for a device that appears to be an orange tree that blooms and produces real fruit in a matter of minutes. But his true creative contribution to automata were three different devices, each featuring a woman and a canary. At the time, it was popular among high-society ladies to have a pet canary and to use an automatic organ called a serinette to teach the bird tunes. In Robert-Houdin’s scenes, the automata women play the serinette multiple times while the automata bird appears to be learning, getting better at the song with each go-round. Other European magicians of the era incorporated automata into their stage shows as well, one even going so far as to steal from Robert-Houdin.

One of Jean-Eugène Robert-Houdin’s magic-show automatons of a woman “teaching” a canary with a serinette.Photo by Via Maison de la Magie
In 1845, German American immigrant Joseph Faber completed his Euphonia, the most impressive talking head yet, a device with a disembodied female head attached to bellows. Demonstrated decades before the telephone, the phonograph, and the wax cylinder were introduced, this automata could speak in multiple languages through the operation of 16 keys assigned a basic sound used in European languages, plus a 17th key that controlled its mechanical glottis.
The Industrial Revolution in France paved the way for the trend of automata as parlor entertainment for adults, starting in the mid-19th century. Until then, larger automata were hand-built to impress royalty while most aristocrats could only afford smaller hand-crafted automata trinkets. The rise of the middle class meant more Europeans were wealthy enough to purchase automata devices to entertain guests at their homes, and advances in manufacturing meant parts for these clockwork robots could be produced and assembled like never before—particularly around Paris, which had the perfect mix of material resources, technology, and skilled craftsman to make these moving works of art. Thus, 1860 to 1910 is known as “The Golden Age of Automata,” and the bulk of the Guinness Collection at the Morris Museum comes from this time period.
“That’s when you saw the very well-known Parisian manufacturers, like Gustave Vichy, Eduoard-Henry Phalibois, Blaise Bontems, Jean Roullet, and his Roullet & Decamps firm, making automata for the middle class,” Ryder says. “At high-end department and toy stores like Au Nain Bleu in Paris, you’d see these exotic, extravagant amusements—toys that really weren’t meant for children. They were aimed at the adult population that was doing the Grand Tour of Europe in the Belle Époque and wanted to go home with a unique souvenir of the region they were visiting. If you visited Switzerland, the country was then internationally known for its timepieces, so you’d buy a clock or watch. The Swiss were also known for their music boxes, invented in 1796, which were manufactured hardly anywhere else, so you might get a music box. But Paris was one of those few places in the world that had the necessary convergence of talent, material, and technology to make automata.
“Parisian manufacturers made up probably 80 percent of the automata market in the late 19th century. There were a few other makers in Germany, Austria, and Czechoslovakia doing something similar, but nowhere near the scale of the half-dozen top Parisian manufacturers.”
The reason Paris became the hotbed of 19th-century automata is that it had gifted artisans in nearly every creative field, as clock-making and mechanical-engineering were not the only skills required to build beautiful automata. Indeed, no one artisan could do it alone.
“So many skills were necessary to create pieces like these,” says Guinness Collection curator Michele Marinelli. “You needed to know metalworking. You needed to be able to create the cams that generate the motion of the piece and the spring motor that drives it. Automata also required other materials like textiles, which is why wives often partnered with their husbands and sewed the costumes for the pieces. Some pieces used materials we would consider exotic, such as tortoiseshell, mother of pearl, furs, feathers, and animal skins, so you would need someone who was skilled in using these materials. It often took multiple people, each working on their specific part, before an automaton could be assembled by the builder, who put his name on it.”
The Parisian automata, like the machines in the Guinness collection, are products of their time, Marinelli explains, when members of the new middle class had the time and money to travel, collect curiosities, and indulge in various amusements. For example, in the first half of the 19th century, circuses and animal menageries were popular attractions, as were taxidermied-filled oddity museums like the American Museum in New York City. After the Civil War ended in 1864, zoological parks and natural history museums began to open in the United States. The anatomy of animals and how they moved were great fascinations.
“Animal figures were very popular as automata,” Marinelli says. “They were often used in animated scenes that showed the creatures exhibiting some kind of humanity or in scenes that told specific stories. Victorians loved animals to the point they stuffed and mounted them, including their dead pets. With many of the singing-bird automata from the era, you’re looking at a real bird that had lived and died. Sometimes the animals with real fur look creepy, and not entirely realistic.”
Monkeys, in particular, appear in many Parisian automata. They’re generally wearing lace collars and fancy velvet dress and engaging in genteel activities. “Think about what happened a hundred years prior to this time period—the French Revolution,” Marinelli says. “When you see a monkey automata dressed like that, the makers are mocking the French aristocracy. It’s a political statement.”
Thanks to all the circuses and pantomimes, clowns were also popular figures. “We have a lot of different clowns in the Guinness collection, performing tricks or things like that,” Marinelli says. “We have a couple Pierrots, which is one of the stock characters from commedia dell’arte—one is sitting on a moon, playing a mandolin. Another Pierrot is sitting at a desk, writing a letter to his love, Columbine.
“Some of them are quite fantastical,” she continues. “We have a clown illusionist by Phalibois who appears to lose his head. We have several other conjurers or magicians. You know the cup-and-ball game, where you lift the cup and there’s a ball underneath, and then when you look under it again, the ball is gone? We have automata that do that. People who see them are amazed.”
Other pieces seem to depict ordinary Victorians engaging in mundane tasks, like dusting parlors or snapping photographs. One of Guinness’ oldest pieces is a chicken that walks, pauses, and lays an egg. “Every automaton tells a story,” Marinelli says. “In a brief moment, it imparts a lot of information to a viewer.”
While these automata delight children, some of them are not exactly G-rated. “We have a chef automata called the Cuisinière,” Marinelli says. “It’s based on a French nursery rhyme, ‘ Le mère Michel’ (‘The mother of Michel the cat’). The chef’s holding a copper pot in one hand. In the other hand, he’s holding a bottle of booze. The chef was having an affair with the lady of the house. Eventually, she rejected him, and he knew there was something that she loved more than him. With this automaton, you see he’s drinking away his sorrows and taking his revenge on her. The lid of the pot rises and a cat pops up. He’s cooking her beloved cat! Of course, if we’re demonstrating that piece when children are present, we modify the story. But kids think it’s hilarious that there’s a cat in the pot.”
Victorians were also fascinated with people from other cultures, but often reduced them to exoticized clichés. “Many of these pieces represent stereotypes and inaccurate information about non-Western cultures,” Marinelli says. “We have a beautiful 3-foot-tall figure called the Mask Seller. If you look closely, you see she’s a Chinese woman wearing Japanese clothing. Again, you’re seeing the perceptions of the Belle Époque Europeans and their Euro-centric understanding of the world.”
The Golden Age of Automata was a time of head-spinning mechanical developments that might feel familiar to us in the Internet Age. Photography, for example, was first introduced in the 1840s. A well-to-do family in the early 1800s might entertain guests with “moving pictures” in zoetropes or by playing songs on giant pinned-cylinder machines known as orchestrions, which could replicate the sounds of an entire orchestra.
By the 1860s, windup clockwork technology was being employed on a smaller scale for children’s toys, made out of stamped-and-lithographed tin by German companies Bing and Märklin. Other toy makers produced mechanical banks whose cast-iron figures were set into motion by depositing a coin. In the 1870s and 1880s, telephones, light bulbs, automobiles, phonographs, and fingered machines that could play pianos were all introduced, as factory workers spent their Sundays at trolley parks where they could ride carousels to the loud sounds of automatic band organs, which often featured quasi-automata musicians.

A Thomas Edison talking phonograph doll that recites “Jack and Jill.”Photo by Via the Smithsonian
The 1890s saw the introduction of player pianos and Edison’s amazing talking doll. Coin-operated vending had evolved into slot machines and coin-operated Mutoscopes and Kinetoscopes that let one person watch short, sometimes sexy, little movies. By the turn of the century, ice-cream parlors and saloons drew customers with coin-operated orchestrions, barrel organs, and player pianos.
Around 1905, penny arcades started to pop up around the United States, many of which featured automata acting out scenes that would be animated by dropping a coin in a slot, as well as coin-op music machines. Some of the most famous coin-op automata of this era include fortune-teller machines like Zoltar and the towering Laffing Sal, which was first made in the 1920s and is thought to be the inspiration for the animatronics you see at Disney theme parks and in Chuck E. Cheese restaurants. Musée Mecanique in San Francisco has a large collection of such early 20th-century coin-op machines.
“The development of coin-operated musical instruments and automata was driven by the vending machine industry, which began in the latter half of the 19th century,” Marinelli says. “Business owners would lease music machines from the manufacturers, who would come to change the music selections, and of course, those companies took half the nickels. But it was worth it for the store owners, because the music brought people in. At the time, there were no jukeboxes or radios, so mechanical music was an amazing experience for customers.
“We have a machine that dates to about 1925, a self-playing violin-piano combination called the Violano Virtuoso, that plays beautifully,” she continues. “It’s electrically powered and, for a nickel, it will play the next song on the 10-song roll. We also have a couple pieces of automata that are coin-operated. One is called the Whistler, which is a boy about 3-foot-tall. He’s inside a glass case, and when you put in a nickel, he whistles a tune for you, so you get both the music and the animation.”
When electronic robots were developed in the 20th century, becoming both reviled and beloved characters in science-fiction, their characteristic stiff, mechanical movement represented a step backward in terms of creating an illusion of life. Even clockwork tin toys regressed, as they were made to imitate the rigid, metallic robots seen in B movies.
“With a real automaton—from the Jaquet-Droz pieces from the late 1700s on through to the Parisian Golden Age between 1850 and 1890—when you wind it up and turn it on, it has an extremely lifelike articulation of movement,” Ryder says. “It’s not jerky, it’s fluid, and so real it’s eerie. It’s only in the last maybe 10 years or so that electronics and processing power can replicate that kind of human fluidity. Old robot tech was better than any new robot tech until very recently.”
Rejecting the Cold War sci-fi mania, in the 1970s, British artists like Sue Jackson, Ron Fuller, Peter Markey, and Paul Spooner began to build old-school automata of animals and humans that were often made of wood and operated by clockwork and hand crank. In 1979, Jackson organized the group into a London collective called Cabaret Mechanical Theatre, which was responsible for a revived interest in automata in the 1980s.
Meanwhile, dystopian science fiction like “Blade Runner” and “Battlestar Galactica” imagined dark futures where artificially intelligent, rebellious robots would be ubiquitous and almost indistinguishable from actual humans. But today, as scientists are developing robots with artificial intelligence for masses, these machines are shedding their humanoid bodies entirely to live in little boxes, like Siri and Alexa do.
Has the dream of re-creating humanity died? Even in the 19th century, German physicist Herman von Helmholtz mused that, for the Gilded Age capitalists bankrolling automation, it was much more efficient to replace human laborers with single-function robots. “Nowadays we no longer attempt to construct beings able to perform a thousand human actions,” Helmholtz wrote, “but rather machines able to execute a single action which will replace that of thousands of humans.”
In spite of these developments, humanoid and animal-like robots are still built and widely adored today. In 2018, the second AutomataCon at the Morris Museum drew more than 300 people, showcasing real, physical androids in all their varied forms—from hand-cranked, hand-carved wooden automata to electronic robots with microprocessors. The makers comprised everyone from woodworkers, jewelers, and steam punks to academics and computer programmers. “The attendees ranged from gray-haired 80-year-olds to little kids participating in our Build Your Own Automata workshop,” Ryder says.
While it’s unlikely we’re ever going to live in a world full of anarchic Replicants or Cylons, androids and other automata serve almost exactly the same purpose today as they did in the 18th and 19th centuries—to astonish and amuse the people who have the privilege of encountering them.
( To learn more about the Golden Age of Automata, visit the Murtogh D. Guinness Collection at the Morris Museum in Morristown, New Jersey. If you buy something through a link in this article, Collectors Weekly may get a share of the sale. Learn more.)
May 1st 2023
The Thoughts of a Spiderweb
Spiders appear to offload cognitive tasks to their webs, making them one of a number of species with a mind that isn’t fully confined within the head.
- Joshua Sokol
More from Quanta Magazine
- This Animal’s Behavior Is Mechanically Programmed
- To Pay Attention, the Brain Uses Filters, Not a Spotlight
- The Year in Biology
Credit: Sin Eater for Quanta Magazine.
Millions of years ago, a few spiders abandoned the kind of round webs that the word “spiderweb” calls to mind and started to focus on a new strategy. Before, they would wait for prey to become ensnared in their webs and then walk out to retrieve it. Then they began building horizontal nets to use as a fishing platform. Now their modern descendants, the cobweb spiders, dangle sticky threads below, wait until insects walk by and get snagged, and reel their unlucky victims in.
In 2008, the researcher Hilton Japyassú prompted 12 species of orb spiders collected from all over Brazil to go through this transition again. He waited until the spiders wove an ordinary web. Then he snipped its threads so that the silk drooped to where crickets wandered below. When a cricket got hooked, not all the orb spiders could fully pull it up, as a cobweb spider does. But some could, and all at least began to reel it in with their two front legs.
Their ability to recapitulate the ancient spiders’ innovation got Japyassú, a biologist at the Federal University of Bahia in Brazil, thinking. When the spider was confronted with a problem to solve that it might not have seen before, how did it figure out what to do? “Where is this information?” he said. “Where is it? Is it in her head, or does this information emerge during the interaction with the altered web?”
In February [2017], Japyassú and Kevin Laland, an evolutionary biologist at the University of Saint Andrews, proposed a bold answer to the question. They argued in a review paper, published in the journal Animal Cognition, that a spider’s web is at least an adjustable part of its sensory apparatus, and at most an extension of the spider’s cognitive system.
This would make the web a model example of extended cognition, an idea first proposed by the philosophers Andy Clark and David Chalmers in 1998 to apply to human thought. In accounts of extended cognition, processes like checking a grocery list or rearranging Scrabble tiles in a tray are close enough to memory-retrieval or problem-solving tasks that happen entirely inside the brain that proponents argue they are actually part of a single, larger, “extended” mind.
Among philosophers of mind, that idea has racked up citations, including supporters and critics. And by its very design, Japyassú’s paper, which aims to export extended cognition as a testable idea to the field of animal behavior, is already stirring up antibodies among scientists. “I got the impression that it was being very careful to check all the boxes for hot topics and controversial topics in animal cognition,” said Alex Jordan, a collective behaviorial scientist at the Max Planck Institute in Konstanz, Germany (who nonetheless supports the idea).
While many disagree with the paper’s interpretations, the study shouldn’t be confused for a piece of philosophy. Japyassú and Laland propose ways to test their ideas in concrete experiments that involve manipulating the spider’s web — tests that other researchers are excited about. “We can break that machine; we can snap strands; we can reduce the way that animal is able to perceive the system around it,” Jordan said. “And that generates some very direct and testable hypotheses.”
The Mindful Tentacle
The suggestion that some of a spider’s “thoughts” happen in its web fits into a small but growing trend in discussions of animal cognition. Many animals interact with the world in certain complicated ways that don’t rely on their brains. In some cases, they don’t even use neurons. “We have this romantic notion that big brains are good, but most animals don’t work this way,” said Ken Cheng, who studies animal behavior and information processing at Macquarie University in Australia.
Parallel to the extended cognition that Japyassú sees in spiders, researchers have been gathering examples from elsewhere in the animal kingdom that seem to show a related concept, called embodied cognition: where cognitive tasks sprawl outside of the brain and into the body.
Perhaps the prime example is another eight-legged invertebrate. Octopuses are famously smart, but their central brain is only a small part of their nervous systems. Two-thirds of the roughly 500 million neurons in an octopus are found in its arms. That led Binyamin Hochner of the Hebrew University of Jerusalem to consider whether octopuses use embodied cognition to pass a piece of food held in their arms straight to their mouths.
For the octopus, with thousands of suckers studding symmetric arms, each of which can bend at any point, building a central mental representation of how to move seems like a computational nightmare. But experiments show that the octopus doesn’t do that. “The brain doesn’t have to know how to move this floppy arm,” Cheng said. Rather, the arm knows how to move the arm.
Readings of electric signals show that when a sucker finds a piece of food, it sends a wave of muscle activation inward up the arm. At the same time, the base of the arm sends another wave of clenched muscles outward, down the arm. Where the two signals meet each other, the arm makes an elbow — a joint in exactly the right place to reach the mouth.
Yet another related strategy, this one perhaps much more common and less controversial, is that the sensory systems of many animals are tuned in to the parts of the world that are relevant to their lives. Bees, for example, use ultraviolet vision to find flowers that have also evolved ultraviolet markings. That avoids the need to take in lots of data and parse it later. “If you do not have those receptors, that part of the world simply doesn’t exist,” said William Wcislo, a behaviorist at the Smithsonian Tropical Research Institute in Panama.
And then there are animals that appear to offload part of their mental apparatus to structures outside of the neural system entirely. Female crickets, for example, orient themselves toward the calls of the loudest males. They pick up the sound using ears on each of the knees of their two front legs. These ears are connected to one another through a tracheal tube. Sound waves come in to both ears and then pass through the tube before interfering with one another in each ear. The system is set up so that the ear closest to the source of the sound will vibrate most strongly.
In crickets, the information processing — the job of finding and identifying the direction that the loudest sound is coming from — appears to take place in the physical structures of the ears and tracheal tube, not inside the brain. Once these structures have finished processing the information, it gets passed to the neural system, which tells the legs to turn the cricket in the right direction.
The Brain Constraint
Extended cognition may partly be an evolutionary response to an outsized challenge. According to a rule first observed by the Swiss naturalist Albrecht von Haller in 1762, smaller creatures almost always devote a larger portion of their body weight to their brains, which require more calories to fuel than other types of tissue.
Haller’s rule holds across the animal kingdom. It works for mammals from whales and elephants down to mice; for salamanders; and across the many species of ants, bees and nematodes. And in this latter range, as brains demand more and more resources from the tiny creatures that host them, scientists like Wcislo and his colleague William Eberhard, also at the Smithsonian, think new evolutionary tricks should arise.
In 2007, Eberhard compared data on the webs built by infant and adult spiders of the same species. The newborns, roughly a thousand times smaller than the adults in some cases, should be under much more pressure from Haller’s rule. As a result, they might be expected to slip up while performing a complex task. Perhaps the spiderlings would make more mistakes in attaching threads at the correct angles to build a geometrically precise web, among other measures. But their webs seemed “as precise as that of their larger relatives,” Eberhard said. “One of the questions is: How do they get away with that?”
Japyassú’s work offers a possible solution. Just as octopuses appear to outsource information-processing tasks to their tentacles, or crickets to their tracheal tubes, perhaps spiders outsource information processing to objects outside of their bodies — their webs.
To test whether this is truly happening, Japyassú uses a framework suggested by the cognitive scientist David Kaplan. If spider and web are working together as a larger cognitive system, the two should be able to affect each other. Changes in the spider’s cognitive state will alter the web, and changes in the web will likewise ripple into the spider’s cognitive state.
Consider a spider at the center of its web, waiting. Many web-builders are near blind, and they interact with the world almost solely through vibrations. Sitting at the hub of their webs, spiders can pull on radial threads that lead to various outer sections, thereby adjusting how sensitive they are to prey that land in those particular areas.
As is true for a tin can telephone, a tighter string is better at passing along vibrations. Tensed regions, then, may show where the spider is paying attention. When insects land in tensed areas of the webs of the orb spider Cyclosa octotuberculata, a 2010 study found, the spider is more likely to notice and capture them. And when the experimenters in the same study tightened the threads artificially, it seemed to put the spiders on high alert — they rushed toward prey more quickly.
The same sort of effect works in the opposite direction, too. Let the orb spider Octonoba sybotides go hungry, changing its internal state, and it will tighten its radial threads so it can tune in to even small prey hitting the web. “She tenses the threads of the web so that she can filter information that is coming to her brain,” Japyassú said. “This is almost the same thing as if she was filtering things in her own brain.”
Another example of this sort of interplay between web and spider comes from the web-building process itself. According to decades of research from scientists like Eberhard, a spiderweb is easier to build than it looks. What seems like a baroque process involving thousands of steps actually requires only a short list of rules of thumb that spiders follow at each junction. But these rules can be hacked from inside or out.
When experimenters start cutting out pieces of a web as it’s being built, a spider makes different choices — as if the already-built portions of silk are reminders, chunks of external memory it needs to retrieve so it can keep things evenly spaced, Japyassú said. Similarly, what happens in a web once it is built can change what kind of web the spider builds next time. If one section of the web catches more prey, the spider may enlarge that part in the future.
And from the opposite direction, the state of a spider’s nervous system can famously affect its webs. Going back to the 1940s, researchers have exposed spiders to caffeine, amphetamines, LSD and other drugs, attracting plenty of media attention along the way. Unsurprisingly, these spiders make addled, irregular webs.
Even skeptics of the extended cognition idea agree that this back and forth between the web and spider is ripe ground for more investigation and debate on how to interpret what the spiders are doing to solve problems. “It introduces a biological setup to the philosophers,” said Fritz Vollrath, an arachnologist at the University of Oxford. “For that, I think it’s very valuable. We can start a discussion now.”
But many biologists doubt that this interplay adds up to a bigger cognitive system. The key issue for critics is a semantic — but crucial — distinction. Japyassú’s paper defines cognition in terms of acquiring, manipulating and storing information. That’s a set of criteria that a web can easily meet. But to many, that seems like a low bar. “I think we’re fundamentally losing a distinction between information and knowledge,” Wcislo said. Opponents argue that cognition involves not just passing along information, but also interpreting it into some sort of abstract, meaningful representation of the world, which the web — or a tray of Scrabble tiles — can’t quite manage by itself.
Further, Japyassú’s definition of cognition may even undersell the level of thought that spiders are capable of, say the spider behaviorists Fiona Cross and Robert Jackson, both of the University of Canterbury in New Zealand. Cross and Jackson study jumping spiders, which don’t have their own webs but will sometimes vibrate an existing web, luring another spider out to attack. Their work suggests that jumping spiders do appear to hold on to mental representations when it comes to planning routes and hunting specific prey. The spiders even seem to differentiate among “one,” “two” and “many” when confronted with a quantity of prey items that conflicts with the number they initially saw, according to a paper released in April.
“How an animal with such a small nervous system can do all this should keep us awake at night,” Cross and Jackson write in an email. “Instead of marveling at this remarkable use of representation, it seems that Japyassú and Laland are looking for an explanation that removes representation from the equation — in other words, it appears they may actually be removing cognition.”
Evolution in the World
Even leaving aside the problem of what cognition actually is, proving the simple version of the argument — that spiders outsource problem solving to their webs as an end run around Haller’s rule — is by itself an empirical challenge. You would need to show that the analytical power of the web saves calories a spider would have otherwise spent on the nervous tissue in a bigger brain, Eberhard said. That would require quantifying how much energy it takes to build and use a web compared with the cost of performing the same operations with brain tissue. Such a study “would be an interesting kind of data to collect,” Eberhard said.
Whether this kind of engineered information-processing happens elsewhere in nature is likewise unclear. Laland is a high-profile advocate for the idea of niche construction, a term from evolutionary theory that encompasses burrows, beaver dams and nests of birds and termites.
Proponents argue that when animals build these artificial structures, natural selection starts to modify the structure and the animal in a reciprocal loop. For example: A beaver builds a dam, which changes the environment. The changes in the environment in turn affect which animals survive. And then the surviving animals further change the environment. Under this rubric, Japyassú thinks, this back-and-forth action makes all niche constructors at least candidates to outsource some of their problem solving to the structures they build, and thus possible practitioners of extended cognition.
Alternatively, more traditional theorists label these structures and spiderwebs alike as extended phenotypes, a term proposed by Richard Dawkins. Extended phenotypes are information from an animal’s genes that they express in the world. For example, bird nests are objects that are somehow encoded in the avian genome. And as with niche construction, natural selection affects the structure — different kinds of birds have evolved to build different kinds of nests, after all. But in the extended phenotype perspective, that selection ultimately just works inward, to tweak the controlling information in the animal’s genome.
It’s a subtle difference. But experts who subscribe to Dawkins’s extended phenotype idea, like Vollrath at Oxford, believe that webs are more like tools the spider uses. “The web is actually a computer, as it were,” he said. “It processes information and simplifies it.” In this view, webs evolved over time like an extension of the spider’s body and sensory system — not so much its mind. Vollrath’s lab will soon embark on a project to test just how webs help the spiders solve problems from the extended phenotype perspective, he said.
While Japyassú, Cheng and others continue to look for extensions of cognition outward into the world, critics say the only really strong case is the one with the most metaphysical baggage: us. “It is conceivable for cognition to be a property of a system with integrated nonbiological components,” Cross and Jackson write. “That seems to be where Homo sapiens is headed.”
Joshua Sokol is a freelance science journalist in Boston.
April 23rd 2023
Starts With A Bang — April 12, 2023
Why atoms are the Universe’s greatest miracle
With a massive, charged nucleus orbited by tiny electrons, atoms are such simple objects. Miraculously, they make up everything we know.

Key Takeaways
- The humble atom is one of the simplest structures in all the Universe, with a tiny, massive nucleus of protons and neutrons orbited by much lighter electrons.
- And yet, perhaps the most miraculous property of our Universe is that it allows the existence of these atoms, which in turn make up some pretty amazing things, including us.
- Are atoms truly the greatest miracle in all of existence? By the end of this article, you just might be convinced.
Share Why atoms are the Universe’s greatest miracle on LinkedIn
One of the most remarkable facts about our existence was first postulated over 2000 years ago: that at some level, every part of our material reality could be reduced to a series of tiny components that still retained their important, individual characteristics that allowed them to assemble to make up all we see, know, encounter, and experience. What began as a simple thought, attributed to Democritus of Abdera, would eventually grow into the atomistic view of the Universe.
Although the literal Greek word “ἄτομος” — meaning “uncuttable” — doesn’t quite apply to atoms, being that they’re made of protons, neutrons, and electrons, any attempt to “divide” the atom further causes it to lose its essence: the fact that it’s a certain, specific element on the periodic table. That’s the essential property that allows it to build up all of the complex structures that exist within our observed reality: the number of protons contained within its atomic nucleus.
An atom is such a small thing that if you were to count up the total number of atoms contained within a single human body, you’d have to count up to somewhere around 1028: more than a million times as great as the number of stars within the entire visible Universe. And yet, just the very fact that we, ourselves, are made of atoms is perhaps the greatest miracle in the entire Universe.
It’s a simple fact that the humble atom is what’s at the core of all the matter we know of within the Universe, from plain old hydrogen gas to humans, planets, stars, and more. Everything that’s made up of normal matter within our Universe — whether solid, liquid, or gas — is made of atoms. Even plasmas, found in very high-energy conditions or in the sparse depths of intergalactic space, are simply atoms that have been stripped of one or more electrons. Atoms themselves are very simple entities, but even with such simple properties, they can assemble to make complex combinations that truly boggle the imagination.
The behavior of atoms is truly remarkable. Consider the following.
- They’re made up of a small, massive, positively charged nucleus, and orbited by a large, low-mass, diffuse cloud of negatively charged electrons.
- When you bring them close to one another, atoms polarize one another and attract, leading to them either sharing electrons together (covalently) or to one atom siphoning one-or-more electrons (ionically) off of the other.
- When multiple atoms bind together, they can create molecules (covalently) or salts (ionically), which can be as simple as having only two atoms bound together or as complex as having several million atoms bound together.

There are two keys to understanding how atoms interact.
- Understanding that each atom is made of electrically charged components: a positively charged nucleus and a series of negatively charged electrons. Even when charges are static, they create electric fields, and whenever charges are in motion, they create magnetic fields. As a result, every atom that exists can become electrically polarized when brought into the presence of an electric field, and every atom that exists can become magnetized when exposed to a magnetic field.
- Understanding, furthermore, that electrons in orbit around an atom will occupy the lowest available energy level. While the electron can be located anywhere in space within about 0.1 nanometers of the atomic nucleus (more or less), it can only occupy a certain set of values as far as energy is concerned, as dictated by the rules of quantum mechanics. The distributions of where these energy-level-dependent electrons are likely to be found are also determined by the rules of quantum mechanics, and obey a specific probability distribution, which is uniquely computable for each type of atom with any arbitrary number of electrons bound to it.

To an extremely good approximation, this view of matter within the Universe:
- that it’s made up of atoms,
- with a heavy, positively charged nucleus and light, negative charges surrounding it,
- that polarize in response to electric fields and that magnetize in response to magnetic fields,
- that can either exchange (ionically) or share (covalently) electrons with other atoms,
- forming bonds, causing polarization and magnetization, and affecting the other atoms around them,
can explain almost everything in our familiar, everyday lives.
Atoms assemble with one another to make molecules: bound states of atoms that fold together in almost innumerable sets of configurations, and that can then interact with one another in a variety of ways. Link a large number of amino acids together and you get a protein, capable of carrying out a number of important biochemical functions. Add an ion onto a protein, and you get an enzyme, capable of changing the bond structure of a variety of molecules.
And if you construct a chain of nucleic acids in just the right order, and you can encode both the construction of an arbitrary number of proteins and enzymes, as well as to make copies of yourself. With the right configuration, an assembled set of atoms will compose a living organism.

If all of human knowledge were someday wiped out in some grand apocalypse, but there were still intelligent survivors who remained, simply passing on the knowledge of atoms to them would go an incredibly long way toward helping them not only make sense the world around them, but to begin down the path of reconstructing the laws of physics and the full suite of the behavior of matter.
The knowledge of atoms would lead, very swiftly, to a reconstruction of the periodic table. The knowledge that there were “interesting” things in the microscopic world would lead to the discovery of cells, of organelles, and then of molecules and their atomic constituents. Chemical reactions between molecules and the associated changes in configurations would lead to the discovery of both how to store energy as well as how to liberate it, both biologically as well as inorganically.
What took human civilization hundreds of thousands of years to achieve could be re-discovered in a single human lifetime, and would bring fascinating hints of more to come when properties like radioactivity or the interaction possibilities between light and matter were discovered as well.
But the atom is also a sufficient key to take us beyond this Dalton-esque view of the world. Discovering that atoms could have different masses from one another but could still retain their elemental properties would lead not only to the discovery of isotopes, but would help investigators discover that atomic nuclei were composed of two different types of particles: protons (with positive charges) as well as (uncharged) neutrons.
This is more profound than almost anyone realizes, at first pass. Within the atomic nucleus, there are:
- two types of component particle,
- of almost-but-not-quite identical masses to one another,
- where the lighter one has a positive charge and the heavier one has a neutral charge,
and that the full nucleus is orbited by electrons: particles that have the equal-and-opposite charge that a proton has, and that have a smaller mass than the mass difference between the proton and the neutron inside the nucleus.
Where, if you take a free proton, it will be stable.
And if you take a free electron, it, too, will be stable.
And then, if you take a free neutron, it won’t be stable, but will decay into a proton, an electron, and (perhaps) a third, neutral particle.

That small realization, all of a sudden, would teach you a tremendous amount about the fundamental nature of reality.
First, it would immediately tell you that there must be some additional force that exists between protons and/or neutrons than the electromagnetic force. The existence of deuterium, for example (an isotope of hydrogen with 1 proton and 1 neutron) tells us that some sort of attractive force between protons and neutrons exists, and that it cannot be explained by either electromagnetism (since neutrons are neutral) or gravity (because the gravitational force is too weak to explain this binding). Some sort of nuclear binding force must be present.
This force must, at least over some small distance range, be able to overcome the electrostatic repulsion between protons within the same atomic nucleus: in other words, it must be a stronger nuclear force than even the (quite strong in its own right) repulsive force between two protons. Because there are no stable atomic nuclei made solely out of two (or more) protons, the neutron must play a role in the stability of the nucleus.
In other words, just from discovering that atomic nuclei contain both protons and neutrons, the existence of the strong nuclear force — or something very much like it — becomes a necessity.

In addition, once one either:
- discovers that the free neutron can decay,
- or discovers radioactive beta decay,
- or discovers that stars are powered by nuclear fusion in their cores,
Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!
Fields marked with an * are required
the implication is immediate for the existence of a fourth fundamental interaction in addition to gravity, electromagnetism, and the strong nuclear force: what we call the weak nuclear force.
Somehow, some sort of interaction must occur that allows one to take multiple protons, fuse them together, and then have it transform into a state that is less massive than the original two protons, where one proton gets converted into at least a neutron and a positron (an anti-electron), and where both energy and momentum are still conserved. The ability to convert one type of particle into another that’s different than “the sum of its parts” or than “the creation of equal amounts of matter-and-antimatter” is something that none of the other three interactions can accommodate. Simply by studying atoms, the existence of the weak nuclear force can be deduced.
In order to have a Universe with many types of atoms, we needed our reality to exhibit a certain set of properties.
- The proton and neutron must be extremely close in mass: so close that the bound state of a proton-and-neutron together — i.e., a deuteron — must be lower in mass than two protons individually.
- The electron must be less massive than the mass difference between the proton and the neutron, otherwise the neutron would be completely stable.
- Furthermore, the electron must be much, much lighter than either the proton or neutron. If it were of comparable mass, atoms would not only be much smaller (along with all the associated structures built out of atoms), but the electron would spend so much time inside the atomic nucleus that the spontaneous reaction of a proton fusing with an electron to produce a neutron would be fast and likely, and that nearby atoms would spontaneously fuse together even under room-temperature conditions. (We see this with laboratory-created muonic hydrogen.)
- And finally, the energies achieved in stars must be sufficient for the atomic nuclei inside them to undergo nuclear fusion, but it cannot be the case that heavier and heavier atomic nuclei are always more stable, otherwise we’d wind up with a Universe filled with ultra-heavy, ultra-large atomic nuclei.
The existence of a Universe rich with a variety of atoms, but dominated by hydrogen, demands all of these factors.

If an intelligent being from another Universe were to encounter us and our reality for the very first time, perhaps the very first thing we’d want to make them aware of was this fact: that we’re made of atoms. That within everything that’s composed of matter in this Universe are tiny, little entities — atoms — that still retain the essential characteristic properties that belong only to that specific species of atom. That you can vary the weight of the nuclei inside these atoms and still get the same type of atom, but if you vary their charge, you’ll get an entirely different atom. And that these atoms are all orbited by the number of negatively charged electrons required to precisely balance the positive charge within the nucleus.
By looking at how these atoms behave and interact, we can understand almost every molecular and macroscopic phenomenon that emerges from them. By looking at the internal components of these atoms and how they assemble themselves, we can learn about the fundamental particles, forces, and interactions that are the very basis of our reality. If there were only one piece of information to pass on to a surviving group of humans in a post-apocalyptic world, there might be no piece of information as valuable as the mere fact that we’re all made of atoms. In some sense, it’s the most miraculous property of all pertaining to our Universe.
April 19th 2023
| The Launchpad SpaceX targeting April 20 for next Starship launch attempt (SpaceX via Twitter) The 62-minute launch window opens Thursday (April 20) at 9:28 a.m. EDT (1328 GMT). Full Story: Space (4/17) NASA eyes more than one moon base for Artemis missions (NASA) NASA’s plan may include more moon bases than you might expect. Full Story: Space (4/18) Space quiz! The Jupiter Icy Moons Explorer (JUICE) spacecraft has taken its first “selfies” from space. How long will JUICE take to get to Jupiter?Learn the answer here! 4 months 8 months 4 years 8 years |
| Space Deal of the Day Best telescopes for kids 2023: Astronomy for all the family (Getty Images) If you’re looking for the best telescopes for kids, you’re in luck as we’ve got a selection of them in this handy guide. Full Story: Space (3/22) |
| Spaceflight Europe’s JUICE Jupiter explorer takes 1st space ‘selfies’ (ESA) The Jupiter Icy Moons Explorer (JUICE) spacecraft has taken its first “selfies” from space, catching stunning images with Earth as a backdrop. Full Story: Space (4/17) Dead NASA satellite will crash to Earth this week (NASA) The 600-pound RHESSI spacecraft is expected to reenter on Wednesday (April 19) at 9:30 p.m. ET, plus or minus 16 hours. Full Story: Space (4/17) |
| Science & Astronomy Giant exoplanet found thanks to star-mapping data (photos) (T. Currie (Subaru/UTSA)) The approach could lead to many more exoplanets being directly detected and imaged. Full Story: Space (4/17) X-ray discovery scores another win for the Big Bang theory (NASA, ESA, M. Postman (STScI) and the CLASH Team) The investigation of real and simulated galactic clusters supports the lambda cold dark matter model of cosmology. Full Story: Space (4/17) |
| Technology Why do JWST images show warped and repeated galaxies? (NASA, ESA, CSA and STScI) The key to weird-looking and repeating galaxies is a phenomenon first predicted by Albert Einstein over 100 years ago. Full Story: Space (4/17) |
April 2nd 2023
PLATO: How an educational computer system from the ’60s shaped the future
Forums, instant messaging, and multiplayer video games all started here.
Cameron Kaiser – 3/17/2023, 11:30 AM

Bright graphics, a touchscreen, a speech synthesizer, messaging apps, games, and educational software—no, it’s not your kid’s iPad. This is the mid-1970s, and you’re using PLATO.
Far from its comparatively primitive contemporaries of teletypes and punch cards, PLATO was something else entirely. If you were fortunate enough to be near the University of Illinois Urbana-Champaign (UIUC) around a half-century ago, you just might have gotten a chance to build the future. Many of the computing innovations we treat as commonplace started with this system, and even today, some of PLATO’s capabilities have never been precisely duplicated. Today, we’ll look back on this influential technological testbed and see how you can experience it now.
From space race to Spacewar
Don Bitzer was a PhD student in electrical engineering at UIUC in 1959, but his eye was on bigger things than circuitry. “I’d been reading projections that said that 50 percent of the students coming out of our high schools were functionally illiterate,” he later told a Wired interviewer. “There was a physicist in our lab, Chalmers Sherwin, who wasn’t afraid to ask big questions. One day, he asked, ‘Why can’t we use computers for education?’”
The system should be, in Sherwin’s words, “a book with feedback.”
The question was timely. Higher education was dealing with a massive influx of students, and with the Soviets apparently winning the space race with Sputnik’s launch in 1957, science and technology immediately became a national priority. “Automatic teaching,” as it was conceived, attracted interest both from academia and the military. Sherwin went to William Everett, the dean of the School of Engineering, who recommended that fellow physicist Daniel Alpert, head of the Control Systems Laboratory, assemble a group of engineers, educators, mathematicians, and psychologists to explore the concept. But the group ran into a serious roadblock in that the members who could teach were unable to comprehend the potential technologies required, and vice versa.
Alpert became exhausted after several weeks of fruitless discussion and was about to terminate the committee until he had an offhand discussion with Bitzer, who claimed to already be “thinking about ways to use old radar equipment as part of an interface for teaching with a computer.” Using grant funding from the US Army Signal Corps, Alpert gave him two weeks, and Bitzer went to work. Advertisement
For the actual processing, Bitzer used the University’s pre-existing ILLIAC I (then just “ILLIAC”) computer. It was the first computer built and owned entirely by an educational institution, and it was a duplicate of the slightly earlier ORDVAC. Both were built in 1952, and they had full software compatibility. IILIAC’s 2,718 vacuum tubes gave it more computing power than even Bell Labs had in 1956, with an addition time of 75 microseconds and an average multiply time of 700 microseconds, 1024 40-bit memory words, and a 10,240-word magnetic drum unit. Bitzer worked with programmer Peter Braunfeld to design the software.

The front end was a consumer TV set wired up with a self-maintaining storage tube display and a small keypad originally used for the Naval Tactical Defense System. On-screen slides appeared from a projector under ILLIAC’s control and were manipulated by the control keys, and ILLIAC could overlay the slides with vector graphics and text at 45 characters per second via what Bitzer and Braunfeld called an “electronic blackboard.” The system offered interactive feedback at a time when most computer interaction was batched. The computer was christened PLATO in 1960 and was later backronymed as “Programmed Logic for Automatic Teaching Operations.” Only one user could run lessons at a time, but the prototype worked.
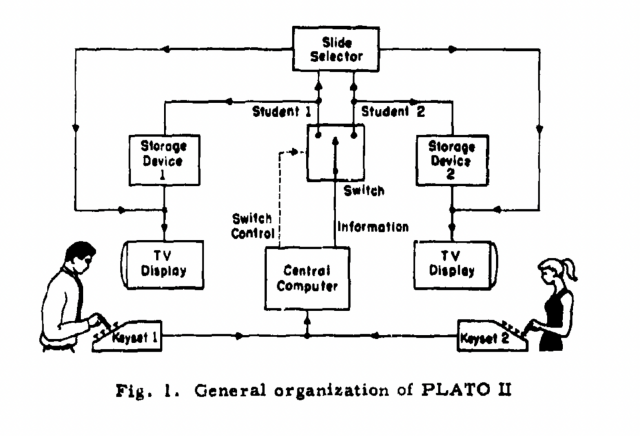
The concept rapidly expanded. In 1961, PLATO II emerged, offering a full alphanumeric keyboard, plus special keys based on the PLATO I’s. These keys included CONTINUE (next slide), REVERSE (previous), JUDGE (check if an answer is correct), ERASE, HELP (for supplementary material or to reveal the answer), and the interesting AHA key for when the student might “suddenly realize the answer to the main-sequence question” and decide to answer it immediately.
Its biggest innovation, though, was time-sharing, allowing multiple students to use the system simultaneously for the first time. Careful programming was required for user time slices so that each session would not drop keystrokes. Unfortunately, ILLIAC’s memory capacity held back this advance, limiting system capacity to just two users at a time and restricting interactivity by capping “secondary help sequences.”
Ars Video
How The Callisto Protocol’s Animations Came To Life With Motion Capture

ILLIAC I was decommissioned in 1963, and PLATO was re-worked yet again. By now, though, the idea was picking up steam and started to attract more funding and outside involvement. The forward-looking architecture of PLATO III took nearly six years to create, starting with a refurbished Control Data Corporation (CDC) 1604 donated the same year to the PLATO group by CDC’s progressive CEO and co-founder William Norris. Norris was intrigued by the social ramifications of wider educational availability and took a personal interest in the group’s work. The CDC 1604-C at the University had a clock speed of 208 kHz and stored 32,768 48-bit words, each word encoding two 24-bit instructions, and its power meant that PLATO lessons could start becoming more sophisticated—and available to larger classes.
There was no facility in those days that could handle simultaneous graphics terminals in significant numbers, so entirely custom system software was developed, along with a specialized authoring language called TUTOR. TUTOR was crafted in 1967 at the new Computer-based Education Research Laboratory (CERL) so that, in Bitzer’s words, “teachers of lesson material [could] function as authors of the material without becoming computer experts.”
Principal architect Paul Tenczar had been unhappy with the level of FORTRAN knowledge required to write lessons for PLATO I and II and wanted to design a “simple users [sic] language… specifically for a computer-based educational system using graphical screen displays.” TUTOR was a mostly imperative, partly declarative language that allowed an educator to define lesson order, screen displays, correct answers and assistive text, such as this example adapted from its 1969 manual:

This snippet shows some of the major features of TUTOR, such as its field-based nature (typical of languages of the day, which were still strongly influenced by punch cards) and unit orientation. A unit could be thought of as a slide (and could even specify a particular slide) with text and figures positioned with WHERE, PLOT, and WRITE statements or drawn with LINEs. HELP, NEXT, and BACK statements defined branching flow from unit to unit. Advertisement
This unit defined two “arrows” where answers were received at particular locations on-screen (an ARROW key on the PLATO III keyboard advanced through them) and defined not only the correct answers (ANS) but words that MUST be present, words that were treated as not salient (DIDDL), and words that CANT be present or are just plain WRONG (including a catch-all for any answer that is incorrect).
Later updates let a specific sentence structure be specified, and the SPELL command even checked for variances in spelling, which, because it was a pedagogical system, would be pointed out to the student. TUTOR programs for PLATO III could store up to 63 typed variables per student as 8-character strings, integers or floating point, and a CALC command allowed computing expressions at runtime. Some of these features are comparable to its better-known contemporary, PILOT, a more typical imperative computer-aided instructional language that evolved into a general-purpose one.
Teachers entered TUTOR programs on a PLATO terminal itself using an editor facility called “author mode.” Author mode was protected by a single global password, so the manual took pains to remind instructors to “[n]ever let any student or other unauthorized individual see how you shift a terminal to AUTHOR MODE.” Besides authoring and loading data to and from disk packs and magnetic tape, an educator could view student progress and print copies. A special “sign in” as a generic STUDENT let an educator preview a lesson, as seen in this mockup of the code above:

PLATO III supported up to 20 simultaneous users to the CDC 1604, and a PLATO III terminal was the first PLATO terminal to exist off-university at Springfield High School in the Illinois state capital. It had a dedicated video downlink and keyboard data uplink. Courses later served not only the University but also a local nursing school, an elementary school, and a community college. By 1970, there were over 720 hours of courseware available.

Of course, education wasn’t the only thing PLATO III was doing. Spacewar! had made a big splash on the PDP-1 in 1962, and Richard Blomme ported it to the network in 1969 using custom character graphics to draw spaceships instead of vectors. Players could duel each other and pick opponents off a “big board.”
It was by no means the last game PLATO users would play.
PLATO IV: The Voyage Home
But many people would never touch a PLATO terminal until PLATO IV. Ever fascinated by the growing possibilities, CDC’s William Norris next set up UIUC in 1968 with a CDC 6400, the smaller, younger sibling of the 60-bit CDC 6600, widely considered to be the world’s first successful supercomputer. The 6600 was one of the first load-store architectures and had 10 parallel functional units for then-unprecedented levels of parallel execution, beating IBM’s monstrous 7030 Stretch with up to three megaFLOPS at 10 MHz to become the fastest computer in the world from 1964 to 1969 until it was eclipsed by its successor, the CDC 7600.
The 6400 may have been the junior member of the family, but it was certainly no slouch. The only difference was a single unified ALU that was nevertheless fully software-compatible with the same memory, I/O, and output capabilities. Norris couldn’t just give away even the baby flagship to the group, but after a meeting with Don Bitzer and Dan Alpert and mindful of the additional grants coming in, he convinced CDC management to let CERL pay nothing the first year and pay in installments thereafter. This provided more than enough power for what Bitzer planned next.
Critically, the success of PLATO’s earlier iterations yielded a dedicated funding stream for Bitzer’s group at CERL from the National Science Foundation, which specified that the new system should support at least 300 terminals. The TUTOR runtime was duly expanded and ported to the 6400, and with sufficient backend power, Bitzer began greatly increasing the front end’s capabilities. Advertisement

Gone was the old cathode-ray storage tube; instead, PLATO IV’s most notable change and enduring feature was a bright orange 512×512 bitmapped gas plasma display first developed in 1964 by Bitzer, electrical engineering professor Gene Slottow, and graduate student Robert Willson. The 8.5-inch-square Digivue display built by glass producer Owens-Illinois in 1971 required no memory nor refresh circuitry, yielding all the advantages of the storage tube but in a durable, flat package with a crisp, high-contrast image. Built-in character and line generators provided hardware-assisted graphics at 180 characters and 600 line-inches per second, using a partially programmable 8×16 252-glyph character set, which student intern Bruce Parello would make into the first digital emoji in 1972.
The display was transparent and could still overlay slides from the projector, which was upgraded to use 4×4-inch microfiche. (Not to be confused with the similar-appearing electroluminescent displays used in systems like the GRiD Compass, orange monochrome gas plasma displays later became popular in the late 1980s and early 1990s for flat-screen portable workstations such as the Compaq Portable 386, the IBM P75, and my personal favorite, the huge 1152×900 garish glow of the 1990 SPARC-based Solbourne S3000. The related Panaplex-style dot matrix plasma display was best known for its wide use in pinball machines until it was replaced by high-intensity LEDs.)

The user interface also improved. Not only was the keyboard revamped, but the display also featured a 16×16 infrared touch panel to let students directly interact with on-screen elements. PLATO IV branched into sound as well, though less successfully. Although a per-terminal pneumatically controlled magnetic disc could hold up to 17 minutes of analogue audio and 4,096 random-access index points, it was unreliable until a 1980 upgrade, and the 1972 specification called it “optional.”
Fortunately, additional client I/O channels meant future upgrades could be installed as capabilities expanded (for example, the parallel port for the audio disc was also used for the 1974 Gooch Synthetic Woodwinds, a simple four-voice music synthesizer, and the follow-on 16-voice Gooch Cybernetic Synthesizer for PLATO V; it was also used for a Votrax speech synthesizer).
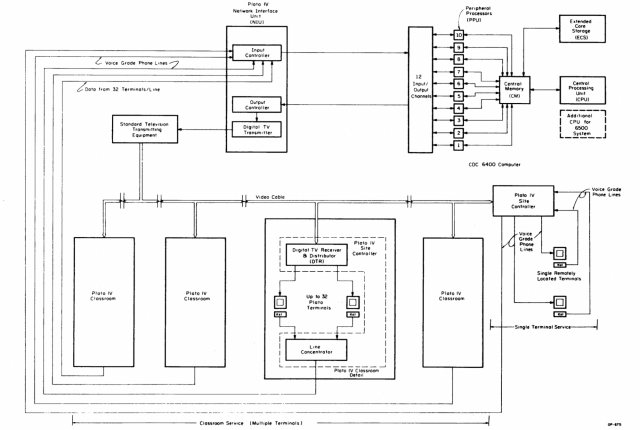
But PLATO IV’s biggest technological leap was probably its massive remote capability, introducing new advances in networking centered on a custom Network Interface Unit (NIU) connected to the CDC 6400. On the server side, course data was stored on a 75-megaword hard disk and three 32 megaword disk packs and was loaded into the 6400’s 64-kiloword central memory and 2-megaword extended core memory to run student sessions. For performance, the extended core served as swap space, not the disks.
The higher-bandwidth downlink from the NIU came via analogue NTSC cable television, using a digital TV receiver and distributor system to demultiplex and serve multiple classroom nodes of up to 32 terminals, each at 1260 bps. Each terminal received a stream of instructions from the receiver/distributor delivered directly to the plasma display and projector; because the terminal could self-maintain its image, no local memory or CPU was required. The lower-bandwidth uplink from each terminal’s keyboard and screen went into the node’s concentrator, which multiplexed their signals and sent them back collectively to the NIU over a single regular voice-grade telephone line, also at 1260 bps.
The downlink/uplink units were collectively referred to as the Site Controller (SC). The 6400’s 12 I/O channels and 10 12-bit peripheral processing units, every bit as powerful as the bigger 6600’s, easily handled the bandwidth of up to 1,008 simultaneous sessions per cable channel, and the use of existing cable and phone lines made network expansion highly feasible. Microwave links could send downlink data en masse to remote sites, or a single remote terminal could receive its own downlink from an SC transmitting over a phone line.
The new terminals were announced as available to all by Bitzer, though the $5,500+ price tag in 1974 per terminal (over $33,000 today) wasn’t particularly egalitarian, and stocks weren’t plentiful. But those who did have access to PLATO had a field day with the new platform, and the freewheeling atmosphere at CERL encouraged new ideas. Besides the notional educational content, a simple message system called “-pad-” sprang up in 1973—implemented as a TUTOR “lesson”—and the concept expanded into the general-purpose Talkomatic group chat written by programmer Doug Brown and later the Term-Talk private chat (named after the TERM key to trigger it). Advertisement
Ostensibly, such features allowed administrators, teachers, and students to communicate productively, consistent with PLATO’s educational aims. But PLATO’s response time was so swift that messaging was practically instantaneous and became highly addictive, and system usage skyrocketed as a result; users hung out in channels waiting for people to drop by to talk to (or sometimes to flirt with). It was a level of interactivity few had ever experienced before, and it represented some of the first social interactions communicated entirely via computer.
Another lasting idea came from 16-year-old student employee David Woolley, who developed the 1973 PLATO Notes bulletin-board system. Originally a project Paul Tenczar assigned him for bug reporting, the system grew into a general message board and then into Kim Mast’s private Personal Notes (“PNOTES”) by the end of 1974, or what we would now call an early form of email. The later Lotus Notes took its name and inspiration from it. Some of its public posts survive in printed form, such as this exchange from January 3, 1974, currently the earliest in the University’s archive:

This line printer was incapable of shifted characters, so the ^ indicated a shift (^7 would be apostrophe on the common non-Selectric keyboards of the day, for example, and ^/ would be a question mark). Infamously, PLATO Notes even inspired early consternation over network censorship during Watergate when the NSF got wind of a Notes discussion about President Nixon’s possible impeachment and promptly called Bitzer (“We just got a call from Nixon’s office. The White House says that our money will disappear if this goes ahead, and we know you’ll disappear…”). Bitzer required the student who started the discussion to post a disclaimer that “it is not permissible in the classroom or on PLATO to organize political mobilization.”
Games started appearing on the system as well. Early PLATO IV users flocked to “big board” listings from which players could choose opponents for chess, dogfighting, and card games, but subsequent diversions were more sophisticated. These included a 1974-5 TUTOR implementation of Dungeons & Dragons (‘dnd’) with the first known game boss and an early roguelike with the opaque name ‘pedit5’ (named after the program slot it was saved to), which author Rusty Rutherford constantly restored despite administrators’ repeated attempts to delete it. There was also 1973’s Empire I, probably the first networked multiplayer arena shooter, written by Iowa State student John Daleske in TUTOR with the assistance of Silas Warner at Indiana University over -pad-. (Silas Warner, inspired by other dungeon games on the platform, later became famous as the designer of Castle Wolfenstein for Muse Software.)
The first 3D flight simulator, Air Race, ran on PLATO IV in 1974; it was also the first multiplayer flight simulator and is believed to be a major influence on UIUC student Bruce Artwick’s home computer Flight Simulator series (itself the ancestor of Microsoft Flight Simulator). Back in Urbana, local high school users started blocking senior users from signing on after hours so they could run large multiplayer games. The problem snowballed to such an extent that Urbana police subsequently asked Bitzer to institute a 9 pm curfew for users under the age of 16. A background program nicknamed “The Enforcer” sought out game sessions during high usage and tried to terminate or disable them with varying success as users started to obfuscate their activities.
As PLATO IV approached commercial quality, the new innovations further interested William Norris at CDC, not only because of the enhanced potential to address social inequity through education but also as a possible new line of business. Norris was increasingly convinced (correctly) that the company needed to diversify from its core hardware concern, especially when chief designer Seymour Cray left to form his own eponymous company in 1972, and he saw PLATO as a means to immediately grow the company’s services portfolio. In 1971, Norris set up a new CDC Educational Department specifically to develop PLATO applications, dogfooding the technology by converting over the corporation’s own training and technical manuals. By 1974, CDC had its own PLATO instance running at its Minneapolis headquarters. Advertisement
In 1976, PLATO had grown to 950 terminals and more than 3,500 hours of instructional material in 100 subjects, served by three instances at UIUC, Florida State University, and CDC itself. UIUC’s instance, now on a donated Cyber 73-2 (an updated equivalent of the CDC 6500 with two one-MIPS CPUs), alone serviced almost 150 locations, including over 30 other colleges and universities. Capacity was getting tight, and Norris made his move. In return for a new top-of-the-line CDC Cyber, Norris wanted all rights to PLATO, period. The University agreed, executing separate agreements on course content, software, and patent licensing, and CERL staff went to the CDC Educational Department to help train them (some stayed on permanently).
The agreement did not terminate CERL, nor did it end Bitzer’s involvement with the project. The agreement permitted CERL to still attract and serve smaller customers, and it continued to do so. As improved microprocessor technology emerged, CERL upgraded the PLATO IV terminal in 1977 with an onboard Intel 8080 CPU, 8K ROM, and 8K RAM that could have code pushed to it by the server; these enhanced terminals—really, early microcomputers—were dubbed “PLATO V” and were the last of the standalone, purpose-built PLATO terminals. Enthusiasts today regard the PLATO V terminals, manufactured by Carroll, as the pinnacle of the design.

For his part, Norris’ belief in PLATO was genuine, and he tirelessly promoted CDC’s new acquisition, declaring that by 1985, it would make up half of the company’s income. CDC even tolerated the games and social applications to a certain extent, considering them value adds, though many clients disabled them. For a variety of reasons, however, CDC used little of the existing content and developed its own over the next several years at sometimes great expense. Some were honorable (re-training unemployed workers for new fields; various courses for inner-city schools), and some were unusual (a farmer crop information system, an Ojibwe Native American language trainer), but despite heavy marketing campaigns, none were highly profitable, even among the large government and corporate customers willing to buy.
The high rates CDC charged clients to recover their operating costs, as well as CDC’s lack of expert courseware writers for some subject areas, were no doubt significant factors. One of its few education successes was online proctored testing, originally developed for the National Association of Security Dealers (today’s FINRA); it was subsequently spun off in 1990 to become the modern Thomson Prometric.
Meanwhile, the microcomputer age was arriving, and Norris decided to take one more leap. It was time to bring PLATO home.
Phenomenal cosmic potential, itty bitty memory space
PLATO V was, of course, technically already a microcomputer, but the terminal-server concept died hard. CERL still sold its own terminals, and CDC started producing the CRT-based IST (“Information System Terminal”) in 1978, but its initial $6,000 price tag (over $24,000 today) made it highly unattractive outside of corporate environments. It was as much an access point for CDC’s other timesharing services as anything else. If PLATO was going to hit the home market, it would simply have to cut the cord. Home computers were also ill-suited to running the length and breadth of what TUTOR was capable of; few could even match the screen resolution, and almost none of them were networked.

In 1979, CERL partnered with CDC to develop the Off-Line PLATO System, an add-on to the PLATO V. Instead of a distant minicomputer managing the session, the V’s 8080 CPU ran everything locally, with lessons on floppy disk. The add-on loaded a list of lessons from the disk and presented students with a menu. A demand paging system read program code and data from the floppy with a latency of approximately a tenth of a second, and variables and student data could be stored on the disk as well.
Even with this concession, there was still no way the PLATO V’s 8-bit CPU with 8K of RAM could handle the entirety of the TUTOR runtime, so CERL pared down TUTOR into μ-TUTOR (Micro-TUTOR), a precompiled bytecode version of TUTOR optimized for paging on small systems. Micro-TUTOR could be written and tested on a full PLATO installation and then compiled for the Off-Line System; lessons distributed in this manner were dubbed Micro-PLATO. The authoring platform evolved into CDC’s PLATO Courseware Development and Delivery system PCD2 (the analogous PCD1 didn’t even need access to PLATO) and later the Micro PLATO Authoring System (MPAS). Advertisement
CDC’s IST-II and IST-III terminals could load and run Micro-TUTOR lessons directly from disks, too, but CDC didn’t sell them as microcomputers. Officially, the first explicit microcomputer to run Micro-PLATO was CDC’s first desktop, the 1981 CDC 110. Like the IST machines it was descended from, it was essentially an overgrown terminal with a Zilog Z80 CPU, 64K of memory, and floppy drives, and BASIC, Pascal, and CP/M were options.
It not only could load offline lessons but still had firmware to dial into PLATO or CDC’s Cybernet and Call 370 timesharing services. CDC didn’t target these machines to home users, either; the ticket price alone was $4,995 (about $16,200 today), plus anywhere from $425 to as much as $4,000 for software, and CDC sold them from its own network of retail Business Centers. The CDC 110’s most immediate descendant was the CDC “Viking” 721, which retained PLATO compatibility.

Instead, the first true home computer port came from Texas Instruments, the first non-CERL, non-CDC machines to run Micro-TUTOR. Texas Instruments was getting deep in the weeds at this point from its protracted market battle with Jack Tramiel’s Commodore Business Machines, and in an effort to elevate itself above its nemesis, the company embarked on the port itself with CDC’s permission in 1981.
Ironically, being a 16-bit system based on the minicomputer-derived 9900 CPU, the Texas Instruments 99/4A was closer to the capabilities of PLATO’s servers than any other home computer at the time, but it still had steep system requirements. The need for a floppy disk drive meant that 99/4A owners had to own an expensive Peripheral Expansion Box as well as the entry-level computer. Released in 1982, the system was strongly modeled on the Off-Line System using a “PLATO in a cartridge” interpreter to run Micro-TUTOR lessons from floppy disk, authored with the new PCD2 system for the lower 256×192 resolution of the 9918 VDP.
CDC’s sole involvement with the TI effort was technical advice and transferring the Micro-TUTOR code to the TI’s floppy disk format; the rest was entirely written by TI. Later that year, however, a different set of Micro-TUTOR courses was announced by CDC itself. A pack of nine courses (basic math, physics, French, German, Spanish, and computer literacy) was announced not only for the “PLATO in a cartridge” TI system, adding to its library, but also for the MOS 6502-based Apple II and Atari 800.
Unlike the TI port, however, the Apple and Atari Micro-PLATO ports were converted to run directly on the computer, and no separate Micro-TUTOR interpreter was used. At $45 for the first lesson and $35 for each additional, the price was high, but PLATO had at last reached home retail. For its part, TI advertised over 100 courses containing over 450 individual lessons by 1983, but it never became more than a niche feature for a struggling system and wasn’t enough to save the home computer line.

CDC tried another tack in 1983 with PLATO Microlink, this time for the IBM PC. Systems with 64K of RAM, a graphics adapter, and a 300 or 1200 baud modem could be turned into PLATO terminals with CDC’s $50 software package, accessing PLATO for a $10 signup fee and $5 an hour during specified times (plus phone charges). Games, messaging, and courseware were all part of the product.
CDC had just been brought on as an investor of online service The Source, and as an enticement to customers who already had online capability, the company offered existing Source subscribers free signup for PLATO. (Although rumors suggested The Source itself would offer PLATO content, this never happened by the time CDC extricated itself from the partnership in 1987.) Inexplicably, despite PC graphic adapters of the time being perfectly capable of using a 512×512 display, the PC client displayed at a scaled 512×256.
Atari, meanwhile, had been working on its own PLATO terminal software as far back as 1981. An early prototype in December of that year became the first non-PLATO microcomputer to access the network, but the unilateral release of CDC’s Micro-PLATO software for the Atari soured the relationship, and negotiations broke down in early 1983. Developer Vincent Wu continued to work on the project on his own time, and when PC Microlink emerged, he was able to convince Atari and CDC management to come back to the table. Advertisement
Finally released in 1984, the Atari PLATO cartridge (named “The Learning Phone”) was explicitly targeted at the home market to avoid cannibalizing PC client sales; CDC resold the PLATO Microlink service to Atari users under the name “PLATO Homelink” for the same price. Like PC Microlink, the Atari PLATO cartridge accessed real PLATO servers via modem and national packet-switched networks. ANTIC’s highest supported resolution was 320×192, so Wu implemented a virtual screen system to either downscale the standard PLATO 512×512 display or zoom in on portions of it. The touchscreen was even emulated with a joystick, making it more compatible with more PLATO lessons than PC Microlink, which had no such capability.
Three uneasy PLATO pieces
Despite these and other efforts, PLATO failed to gain traction in the home market, and amid substantial financial turmoil at CDC, William Norris stepped down as CEO in 1986. PLATO’s foundering wasn’t the only thing damaging CDC’s bottom line, but observers agreed it was a notable part of it. Norris alleged Micro-TUTOR and Micro-PLATO got the project off track and blamed poor market choices with TI and Atari for its woes. Indeed, the Apple II never got a native PLATO or Micro-PLATO client despite its ubiquitous presence in American schools, nor did the Commodore 64, then the dominant leader in the home market. Don Bitzer was less charitable, blaming CDC’s ossified governance structure and excessively high content development costs for PLATO’s decline instead.
In an attempt to reorganize, new CEO Lawrence Perlman began liquidating assets, including the Commercial Credit Corporation branch in 1986 (to become Citigroup), their portion of The Source in 1987 (killed by CompuServe), and Ticketron in 1990 (now part of Ticketmaster). In 1989, CDC sold the PLATO trademark and a portion of its courseware markets to investor William Roach and his Roach Organization, which renamed it TRO Learning in 1992 and focused on corporate training. Despite being renamed again to PLATO Learning in 2000, PLATO sensu stricto was never used by the company, and very little of the original divestment actually persisted. It was eventually renamed a final time to Edmentum in 2012 and is still in business today, primarily serving school districts.
Microlink having already been shut down, the remaining portion of PLATO at CDC was renamed to CYBIS (CY-ber Based Instructional System) to service the company’s existing commercial and government contracts. In 1992, CDC spun out its computer services line as Control Data Systems, which eventually sold CYBIS in 1994 to startup University Online, Inc. UOL renamed itself to VCampus in 1996 and subsequently went out of business (the domain name today is parked).
CDS was absorbed into BT (the former British Telecom) in 1999, marking the end of Control Data’s technology under that name. CDC’s last true surviving successor after the breakup is HR services and software corporation Ceridian, today still in operation in CDC’s old home town of Minneapolis.
In the midst of all this, the CERL group at UIUC continued to quietly maintain its academic customers and develop its own courseware as permitted by the 1976 agreement with CDC. In 1985, CERL founded the for-profit business University Communications, Inc. (UCI) to monetize those operations. The most lasting remnant to emerge from this twilight was NovaNET, which expanded the cable TV-based downlink from the PLATO instance to the classroom with a new satellite option (a modem still provided the uplink) and serviced an increasingly diverse clientele that even included juvenile halls.
Unfortunately for CERL, Don Bitzer’s departure from the university in 1989 meant the group had lost its most ardent defender, and CERL was disbanded in 1994. UCI itself was spun off entirely from the university and reincorporated as NovaNET Learning. This initial piece was bought by National Computer Systems, and then NCS itself was bought by Pearson Education in 1999.
While some form of TUTOR still underlaid the system, NovaNET enhanced it most notably with a more modern user interface and greater multimedia capabilities delivered over a conventional LAN via an updated Microsoft Windows client. Its biggest success was in alternative education, where Pearson marketed the “learn at your own pace” architecture to students poorly served by a conventional classroom experience (actual research on its effectiveness was somewhat more equivocal). As PCs became individually more powerful, however, and courseware transitioned to fat clients and web-based trainings, the proprietary centralized nature of NovaNET’s offering became an increasing disadvantage, and customers gradually left the network. In 2015, Pearson decommissioned NovaNET, the last of the direct PLATO descendants. Advertisement
PLAy TOday
But even if you weren’t around for PLATO in its prime, that doesn’t mean you’ll never get to experience it. After VCampus went under, the business and assets reverted to its former CEO, who granted permission for a non-commercial release of CYBIS. One such instance is Cyber1, which maintains a public instance accessible over the Internet using the open source PTerm client, available for Windows, macOS (including Power Macs), and Linux. PTerm adds color support and can even execute Micro-TUTOR lessons from disk images. Much of the experience from PLATO’s heyday, including its famous games, are available.
More interested in the backend? Run your own installation on top of the dtCYBER package, which emulates a CDC 6600-compatible Cyber 175. The package includes a CYBIS disk image with CDC’s NOS operating system, a boot tape image, and PTerm.
And if you want a more modern retrocomputing take, IRATA.ONLINE is a PLATO-based system with new content focused on old machines, starting originally with clients for Atari 8-bits (including, with interfacing, Atari’s old 1984 cartridge, but also FujiNet) and now Apple II and IIGS, Commodore 64 and 128 (VDC supported for full resolution), IBM 5150 PC and PCjr, ZX Spectrum (serial or Spectranet), Atari ST, Amiga, TI 99/4A, and many more. It also works with PTerm, and source code is available.
PLATO’s contributions to computer-aided education can’t be overemphasized, but the advances to make those contributions possible led to critical innovations in many other technical fields as well, such as graphic displays, networking, and user interfaces. In addition, the creativity of its users and its early freewheeling environment combined to yield groundbreaking academic content, highly influential games, and pioneering social and messaging tools that were the conceptual forerunners of the applications we use now and set in motion the cultural underpinnings of our ubiquitously networked modern world.
Thanks to the dedicated preservationists maintaining the software and committing its rich history to posterity, PLATO lives on to teach, inspire, and entertain today’s generation and the generations to come, even years after the organizations that spawned it have faded away.
Cameron Kaiser works in public health by day and in a wonderland of geriatric technology by night. His lab in Southern California is likely where your old computer lives again. Read about his other retrocomputing adventures at Old Vintage Computing Research.
March 15th 2023
| History & Archaeology |
| ‘Perfect’ 1st edition of Copernicus’ controversial book on astronomy could fetch $2.5 million (Sophia Rare Books) A first edition of Nicolaus Copernicus’ groundbreaking work, in which the Polish astronomer proposed that the Earth revolved around the sun and not vice versa, will be going up for sale next month. It is expected to fetch $2.5 million. Full Story: Live Science (3/14) |
March 14th 2023
3 unexplainable mysteries of life on Earth
Earth, for all we know, is the only planet with life on it. But how did it start?

The defining feature of our world is life. For all we know, Earth is the only planet with life on it. Despite our age of environmental destruction, there’s life in every corner of the globe, under its water, nestled in the most extreme environments we can imagine.
But why? How did life start on Earth? What was the series of events that led to birds, bugs, amoebas, you, and me?
That’s the subject of Origins, a three-episode series from Unexplainable — Vox’s podcast that explores big mysteries, unanswered questions, and all the thingswelearn by diving into the unknown.
The quest of discovering the “how” of life on Earth is bigger than just filling in the missing chapters of the history book of our world. To search for the origins of life on Earth is to ask other big questions: How rare is it for life to form on any planet? How improbable is it for life to form on any planet, anywhere?
We don’t have all the pieces of the story, but what we do know tells an origin story of epic scope that takes us on an adventure to the primordial days of our world.
It all starts with water.
1) Where did Earth’s water come from?
:no_upscale()/cdn.vox-cdn.com/uploads/chorus_asset/file/24467005/458847426.jpg)
The quest to understand why there is life on Earth must start with water because water is the one thing on Earth all life needs. Different forms of life can survive on extremely different food sources, but nothing lives without water.
So it’s curious that scientists don’t fully understand how water came to cover two-thirds of the surface of our world and create the very first condition necessary for life.
The problem is simple. When the Earth was forming, it was extremely hot. Any water that was around at the beginning would have boiled away.
“So how do you get so much liquid condensing onto the surface of a planet that should be really, really hot?” Lydia Hallis, a planetary scientist at the University of Glasgow, tells Unexplainable’s Noam Hassenfeld.
Scientists can think of a few plausible options. Was it delivered by comets crashing into our world? Or more fantastically, do we only have water due to the extremely circumstantial event of planets like Jupiter wandering toward the sun from the outer solar system? Or was it, somehow, deeply buried within the early Earth?
Hallis has been traveling the world to investigate and try to find some samples of the very oldest water on Earth. Here’s what she’s learned so far:
2) How did life start in that water?
:no_upscale()/cdn.vox-cdn.com/uploads/chorus_asset/file/24467042/857129344.jpg)
Once there was water, somehow there was life. It’s possible that life didn’t start on Earth at all. But scientists have good reason to suspect it did.
For decades, scientists have been trying to recreate in labs the conditions of that early water-filled Earth. The thinking is, perhaps if they can mimic the conditions of the early Earth, they will eventually be able to create something similar to the first simple cells that formed here billions of years ago. From there, they could piece together a story about how life started on Earth.
This line of research has demonstrated some stunning successes. In the 1950s, scientists Harold Urey and Stanley Miller showed that it’s possible to synthesize the amino acid glycine — i.e. one of life’s most basic building blocks — by mixing together some gasses believed to have filled the atmosphere billions of years ago, with heat and simulated lightning.
Since then, scientists have been able to make lipid blobs that looked a lot like cell membranes. And they’ve gotten RNA molecules to form, which are like simplified DNA. But getting all these components of life to form in a lab and assemble into a simple cell — that hasn’t happened.
So what’s standing in the way? And what would it mean if scientists actually succeed and create life in a bottle? They could uncover not just the story of the origin of life on Earth, but come to a shocking conclusion about how common life must be in the universe.
Unexplainable’s Byrd Pinkerton explores in this episode:
3) What is life anyway?
:no_upscale()/cdn.vox-cdn.com/uploads/chorus_asset/file/24467037/104727898.jpg)
However life first started, today we know Earth is teeming with it. We know life when we see it. But do we know what life fundamentally is?
No.
“No one has been able to define life, and some people will tell you it’s not possible to,” says Carl Zimmer, science reporter and author of Life’s Edge: The Search for What it Means to be Alive.
That’s not for a lack of trying. “There are hundreds, hundreds of definitions of life that scientists themselves have published in the scientific literature,” Zimmer says.
This question — what is life — feels like it should be easy, something a fifth grader ought to answer. “It does feel like it should be easy because we feel it,” Zimmer says. “Our brains are actually tuned to recognizing things like biological motion. We’re sort of hardwired for recognizing life. But that doesn’t actually mean that we know what it is.”
The problem is, for each definition of life, scientists can think of a confounding exception. Take, for instance, NASA’s definition of life: “Life is a self-sustaining chemical system capable of Darwinian evolution.” But that definition would exclude viruses, which are not “self-sustaining” and can only survive and replicate by infiltrating a host.
On one hand, a definition of life would come in handy as we’re searching for signs of it on other planets and moons. How would we know life when we found it? On the other hand, Zimmer explains, perhaps it’s just not possible to define life — at least not with our current knowledge.
Carl Zimmer explains on an episode airing Wednesday, March 15.
March 13th 2023
Back to the father: the scientist who lost his dad – and resolved to travel to 1955 to save him
After losing his beloved father when he was 10, Ronald Mallett read HG Wells and Einstein. They inspired his eminent career as a theoretical physicist – and his lifelong ambition to build a time machine
Prof Ronald Mallett thinks he has cracked time travel. The secret, he says, is in twisting the fabric of space-time with a ring of rotating lasers to make a loop of time that would allow you to travel backwards. It will take a lot more explaining and experiments, but after a half century of work, the 77-year-old astrophysicist has got that down pat.
His claim is not as ridiculous as it might seem. Entire academic departments, such as the Centre for Time at the University of Sydney, are dedicated to studying the possibility of time travel. Massachusetts Institute of Technology (MIT) is working on a “time-reversal machine” to detect dark matter. Of course there are still lots of physicists who believe time travel, or at least travelling to the past, is impossible, but it is not quite the sci-fi pipe dream it once was.
However, the story of how Mallett, now emeritus professor at the University of Connecticut, reached this point could have been lifted straight from a comic book. A year after losing his father, Boyd, at the age of 10, Mallett picked up a copy of HG Wells’s The Time Machine and had an epiphany: he was going to build his own time machine, travel back to 1955 and save his father’s life.
Mallett still idolises his dad, and thinks about him every day. He had been exceptionally close to Boyd, whom he describes as a handsome, erudite and funny “renaissance man” who would try to inspire curiosity in Mallett and his two brothers and sister. “When he passed away, it was like this light went out. I was in shock,” Mallett says down the line from his study in Connecticut.
Boyd had gone to bed with his wife, Dorothy, on the night of their 11th wedding anniversary and let out a deep sigh. It was only when she nudged him and his head flopped off his pillow “like a sack of flour” that Dorothy realised something was wrong. Mallett woke later that night to his mother crying uncontrollably and the news that his father had died of a heart attack. “I couldn’t comprehend how this was possible. To this day, it’s hard for me to believe he’s gone. Even after 60 some years,” he says.
One of the great pleasures for me was meeting Dad when he got off the subway and carrying his toolbox home
Boyd had fought in the second world war and then, on his return home, used the GI bill, which helped qualifying military veterans with their tuition fees, to retrain in electronics. He would bring home gyroscopes and crystal radio sets, taking them apart and explaining how they worked to his children. After the family moved to a new apartment complex in the Bronx in the late 40s, Boyd took on work as a TV repairman.
“I adored him,” says Mallett. “One of the great pleasures for me was meeting him when he got off the subway and carrying his toolbox home with him. He just literally lit up the room when he would come in.”
Even though Boyd earned a modest living, he spoiled his children and their mother. “He worked very, very hard, he loved having a family, and he loved playing with us,” Mallett says. “One of the last things that I remember was – [on] one of the last Christmases – we wanted a bike, and he took on extra work. And all three boys got a bicycle; it was incredible for him to do that.”

Rod Taylor in the 1960 film of The Time Machine – the book made a huge impression on Mallett when he was grieving for his dad as a boy. Photograph: Allstar Picture Library Limited./Alamy
After Boyd died, the bubble of safety he had created for his family vanished. Dorothy and the children moved to Altoona, Pennsylvania, to be closer to her parents. One day, as Mallett and his brothers were walking around their new neighbourhood to meet friends, they saw four white boys playing nearby and approached them to say hello. When they got closer, one of the kids spat the N-word at them. No one had ever called Mallett that before. Something in him snapped and he punched the boy until he apologised. “I was in the dark already. And that just added to that, I think. I was becoming unravelled because I was in a very deep depression after he died,” says Mallett.
Mallett never had cause to contemplate his race in the Bronx. “The neighbourhood that we lived in was predominantly a white Jewish neighbourhood. And I’d never experienced any feeling of prejudice. I was actually the only African American in the predominantly white Jewish Boy Scout troop, and I felt I was not treated any differently from any of the others,” he says.
Mallett became a truant and withdrew into the comforting fantasy world of books and magazines. One of these books was The Time Machine. “It somehow just spoke to me,” he says. “The very first paragraph changed my life. I still remember the quote: ‘Scientific people know very well that time is just a kind of space and we can move forward and backwards in time, just as we can in space.’” Inspired by the picture of the time machine on his illustrated copy, Mallett cobbled together a replica from his bicycle and his dad’s spare TV and radio parts. But, of course, it didn’t work.
In films, travelling through time is as easy as sharing a phone box with George Carlin, à la Bill and Ted; hitting 88mph in a DeLorean kitted out with a flux capacitor as in Back to the Future; or spilling a supercharged energy drink over a hot tub’s control panel,as in the 2010 film Hot Tub Time Machine. In reality, it’s slightly trickier. Well, travelling into the future is easy – we’re all doing it now in fact – but going back in time presents a far bigger problem.
Reading Einstein at 11 made Mallett realise there are ways time could be altered. Photograph: Bettmann/Bettmann Archive
Undeterred, Mallett kept reading. He came across an Einstein paperback. Even at age 11 he got the gist that, according to Einstein, time is not absolute. Mallett rationalised that the key to seeing his dad again was understanding everything in that book, so back to school he went, rising quickly to the top of his classes and graduating with straight As. Without the funds to go straight on to college, he joined the air force, intending to use the GI bill as his father had. “It was a very, very solitary life,” he says. He chose the graveyard shift so that he could study and “was just in my world, in my books”.
After the air force, Mallett enrolled at Pennsylvania State University and became one of the first African Americans to receive a PhD in physics. However, despite his academic success, he didn’t have the confidence to publicly discuss time travel. It was the 1980s and talking about it was still unheard of in “serious” academic circles; doing so could be career suicide. Plus, growing up in white America had taught him that no matter how high he climbed, he was still in danger of being disrespected.
It wasn’t until the mid-90s, when people were starting to talk about the possibility of time travel, that Mallett felt ready to be more open about his endeavour. Heart problems meant he had to have angioplasty surgery and he spent his months of recovery poring over his research. Mallett found his eureka moment in a black hole.
“It turns out that rotating black holes can create a gravitational field that could lead to loops of time being created that can allow you to go to the past,” says Mallett. Unlike a normal black hole, a spinning black hole has two event horizons (the surface enclosing the space from which electromagnetic radiation cannot escape), an inner one and an outer one. Between these two event horizons, something called frame dragging – the dragging of space-time – occurs.

Prof Mallett draws a diagram of his ring laser at the University of Connecticut, 2015. Photograph: Bloomberg/Getty Images
“Let me give you an analogy,” Mallett says, with patience. “Let’s say you have a cup of coffee in front of you right now. Start stirring the coffee with the spoon. It started swirling around, right? That’s what a rotating black hole does.” But, he continues, “in Einstein’s theory, space and time relate to each other. That’s why it’s called space-time. So as the black hole is rotating, it’s actually going to cause a twisting of time.”
Although black holes are in short supply in this corner of the Milky Way, Mallett thinks he may have found an artificial alternative in a device called a ring laser, which can create an intense and continuous rotating beam of light – “light can create gravity … and if gravity can affect time, then light itself can affect time,” he explains.
Some of Mallett’s critics have objected that his time machine would have to be the size of the known universe, thus completely impractical. I put this to him. “You’re absolutely right; you’re talking about galactic types of energy in order to do that,” he acknowledges.
So, how big would your time machine be? “I don’t know that yet. The thing is that what is necessary first is being able to show that we can twist space – not time – twist space with light.” Only then, he says, will he know what is necessary to do the rest. Mallett likens it to asking the Wright brothers, straight after their maiden flight, for their predictions for how humans will reach the moon. All Mallett can tell us at the moment is that his time machine, however big, will look like a cylinder of rotating light beams.

Such an endeavour would, of course, not come cheap, but it’s highly unlikely that any government would pour its resources into time travel, and the only billionaire wacky enough to potentially fund such a project is busy with Mars and Twitter. Plus, here’s the rub. Even if clever engineers and barmy billionaires put Mallett’s theories into practice, it would only allow travel back in time to the point when the time loop was created, which could never be 1955. For all Mallett’s work and theories, there is no possibility of him travelling back to see his dad again.
How did he feel when he realised? “It was sad for me but it wasn’t tragic, because I remember that there was this little boy who dreamed of the possibility of having a time machine. I have figured out how it can be done.” Mallett also takes comfort in the enormous potential his machine could have for the wellbeing of life on our planet. “Let’s suppose that we had already had this device going on some years ago, and now we have medicines that can cure Covid. Imagine if we could predict precisely when earthquakes are going to occur, or tsunamis. So, for me, I’ve opened the door to the possibility. And I think that my father would have been really proud about that.”
February 25th 2023
- Podcasts
- Video
- Artificial Intelligence
- Climate
- Games
- Newsletters
- Magazine
- Events
- Wired Insider
- Jobs
- Coupons
Winter Sale: Get WIRED for just $29.99 $5. Plus, get free stickers! Subscribe now.

Winter Sale: Get WIRED for just $29.99 $5
Get unlimited access to WIRED.com and exclusive subscriber-only content for less than $1 per month.
Plus, get free stickers! Ending soon.

Feb 10, 2023 7:00 AM
The Generative AI Race Has a Dirty Secret
Integrating large language models into search engines could mean a fivefold increase in computing power and huge carbon emissions.
In early February, first Google, then Microsoft, announced major overhauls to their search engines. Both tech giants have spent big on building or buying generative AI tools, which use large language models to understand and respond to complex questions. Now they are trying to integrate them into search, hoping they’ll give users a richer, more accurate experience. The Chinese search company Baidu has announced it will follow suit.
But the excitement over these new tools could be concealing a dirty secret. The race to build high-performance, AI-powered search engines is likely to require a dramatic rise in computing power, and with it a massive increase in the amount of energy that tech companies require and the amount of carbon they emit.
“There are already huge resources involved in indexing and searching internet content, but the incorporation of AI requires a different kind of firepower,” says Alan Woodward, professor of cybersecurity at the University of Surrey in the UK. “It requires processing power as well as storage and efficient search. Every time we see a step change in online processing, we see significant increases in the power and cooling resources required by large processing centres. I think this could be such a step.”
Training large language models (LLMs), such as those that underpin OpenAI’s ChatGPT, which will power Microsoft’s souped-up Bing search engine, and Google’s equivalent, Bard, means parsing and computing linkages within massive volumes of data, which is why they have tended to be developed by companies with sizable resources.
“Training these models takes a huge amount of computational power,” says Carlos Gómez-Rodríguez, a computer scientist at the University of Coruña in Spain.“Right now, only the Big Tech companies can train them.”
While neither OpenAI nor Google, have said what the computing cost of their products is, third-party analysis by researchers estimates that the training of GPT-3, which ChatGPT is partly based on, consumed 1,287 MWh, and led to emissions of more than 550 tons of carbon dioxide equivalent—the same amount as a single person taking 550 roundtrips between New York and San Francisco.
Featured VideoRE:WIRED GREEN 2022: James McBride on Decarbonizing the World
Most Popular
- CultureThe Last of Us Signals the End of an EraAngela Watercutter
- BusinessAmazon Has a Donkey Meat ProblemDhruv Mehrotra
- BusinessWorkers Are Dying in the EV Industry’s ‘Tainted’ CityPeter Yeung
- BackchannelThe Battle for the Soul of Buy NothingVauhini Vara
“It’s not that bad, but then you have to take into account [the fact that] not only do you have to train it, but you have to execute it and serve millions of users,” Gómez-Rodríguez says.
There’s also a big difference between utilizing ChatGPT—which investment bank UBS estimates has 13 million users a day—as a standalone product, and integrating it into Bing, which handles half a billion searches every day.
Martin Bouchard, cofounder of Canadian data center company QScale, believes that, based on his reading of Microsoft and Google’s plans for search, adding generative AI to the process will require “at least four or five times more computing per search” at a minimum. He points out that ChatGPT currently stops its understanding of the world in late 2021, as part of an attempt to cut down on the computing requirements.
In order to meet the requirements of search engine users, that will have to change. “If they’re going to retrain the model often and add more parameters and stuff, it’s a totally different scale of things,” he says.
That is going to require a significant investment in hardware. “Current data centers and the infrastructure we have in place will not be able to cope with [the race of generative AI],” Bouchard says. “It’s too much.”
Data centers already account for around one percent of the world’s greenhouse gas emissions, according to the International Energy Agency. That is expected to rise as demand for cloud computing increases, but the companies running search have promised to reduce their net contribution to global heating.
“It’s definitely not as bad as transportation or the textile industry,” Gómez-Rodríguez says. “But [AI] can be a significant contributor to emissions.”
Microsoft has committed to becoming carbon negative by 2050. The company intends to buy 1.5 million metric tons worth of carbon credits this year. Google has committed to achieving net-zero emissions across its operations and value chain by 2030. OpenAI and Microsoft did not respond to requests for comment.
See What’s Next in Tech With the Fast Forward Newsletter
From artificial intelligence and self-driving cars to transformed cities and new startups, sign up for the latest news.
Your email
By signing up you agree to our User Agreement (including the class action waiver and arbitration provisions), our Privacy Policy & Cookie Statement and to receive marketing and account-related emails from WIRED. You can unsubscribe at any time.
The environmental footprint and energy cost of integrating AI into search could be reduced by moving data centers onto cleaner energy sources, and by redesigning neural networks to become more efficient, reducing the so-called “inference time”—the amount of computing power required for an algorithm to work on new data.
“We have to work on how to reduce the inference time required for such big models,” says Nafise Sadat Moosavi, a lecturer in natural language processing at the University of Sheffield, who works on sustainability in natural language processing. “Now is a good time to focus on the efficiency aspect.”
Google spokesperson Jane Park tells WIRED that Google was initially releasing a version of Bard that was powered by a lighter-weight large language model.
“We have also published research detailing the energy costs of state-of-the-art language models, including an earlier and larger version of LaMDA,” says Park. “Our findings show that combining efficient models, processors, and data centers with clean energy sources can reduce the carbon footprint of a [machine learning] system by as much as 1,000 times.”
The question is whether it’s worth all the additional computing power and hassle for what could be, in the case of Google at least, minor gains in search accuracy. But Moosavi says that, while it’s important to focus on the amount of energy and carbon being generated by LLMs, there is a need for some perspective.
“It’s great that this actually works for end users,” she says. “Because previous large language models weren’t accessible to everybody.”
More Great WIRED Stories
- 📩 The latest on tech, science, and more: Get our newsletters!
- The out-of-control spread of crowd-control tech
- The future of weight loss looks like its past
- An inflammatory disease is hiding in plain sight
- Rihanna pioneered a new kind of Super Bowl show
- Bitcoin miners are playing a risky game of chicken
- 👁️ Explore AI like never before with our new database
- ✨ Optimize your home life with our Gear team’s best picks, from robot vacuums to affordable mattresses to smart speakers
Chris Stokel-Walker is a freelance journalist and WIRED contributor. He is the author of YouTubers: How YouTube Shook up TVand Created a New Generation of Stars, and TikTok Boom: China’s Dynamite App and the Superpower Race for Social Media. His work has also appeared in TheNew York Times,… Read more
TopicsChatGPTalgorithmsartificial intelligenceclimate changeenvironmentMore from WIRED
Chatbots Got Big—and Their Ethical Red Flags Got Bigger
Researchers have spent years warning that text-generation algorithms can spew bias and falsehoods. Tech giants are rushing them into products anyway.
Khari Johnson
The Race to Build a ChatGPT-Powered Search Engine
A search bot you converse with could make finding answers easier—if it doesn’t tell fibs. Microsoft, Google, Baidu, and others are working on it.
Will Knight
Generative AI Is Coming For the Lawyers
Large law firms are using a tool made by OpenAI to research and write legal documents. What could go wrong?
Chris Stokel-Walker
One Startup’s Plan to Help Africa Lure Back Its AI Talent
Lelapa is building a research lab to serve African businesses and nonprofits, with the hope that locally grown algorithms can better serve communities.
Khari Johnson
The Chatbot Search Wars Have Begun
Microsoft, Google, and China’s Baidu all showed off ChatGPT-inspired technology to reinvent web search this week.
Will Knight
Fact-Checkers Are Scrambling to Fight Disinformation With AI
Bad actors use artificial intelligence to propagate falsehoods and upset elections, but the same tools can be repurposed to defend the truth.
Lydia Morrish
The WIRED Guide to Artificial Intelligence
Supersmart algorithms won’t take all the jobs, But they are learning faster than ever, doing everything from medical diagnostics to serving up ads.
Tom Simonite
Roblox Is Bringing Generative AI to Its Gaming Universe
The company aims to draw on the new technology’s code-writing ability to make its digital worlds even more customizable.
Will Knight
Get 1 year for $29.99 $5
WIRED is where tomorrow is realized. It is the essential source of information and ideas that make sense of a world in constant transformation. The WIRED conversation illuminates how technology is changing every aspect of our lives—from culture to business, science to design. The breakthroughs and innovations that we uncover lead to new ways of thinking, new connections, and new industries.
More From WIRED
Contact
© 2023 Condé Nast. All rights reserved. Use of this site constitutes acceptance of our User Agreement and Privacy Policy and Cookie Statement and Your California Privacy Rights. WIRED may earn a portion of sales from products that are purchased through our site as part of our Affiliate Partnerships with retailers. The material on this site may not be reproduced, distributed, transmitted, cached or otherwise used, except with the prior written permission of Condé Nast. Ad Choices
Select international site
February 20th 2023.
There’s a Chance the Black Hole at the Center of Our Galaxy Is Actually a Wormhole
The odds are slim, but a new analysis shows it’s possible.

- Charlie Wood
Science fiction writers love wormholes because they make the impossible possible, linking otherwise unreachable places together. Enter one, and it’ll spit you back out in another locale—typically one that’s convenient for the plot. And no matter how unlikely these exotic black hole relatives are to exist in reality, they tend to fascinate physicists for exactly the same reason. Not long ago, some of those physicists took the time to ponder what such a cosmic shortcut might look like in real life, and even make a case that there could be one at the center of our galaxy.
The most surefire way to confirm a wormhole’s existence would be to directly prod a black hole and see if it’s hiding a bridge to elsewhere, but humanity may never have that opportunity. Even so, researchers could rule out some of the most obvious scenarios from Earth. If the monster black hole residing in the churning center of the Milky Way, for instance, is more door than dead end, astronomers could tease out the presence of something on the other side. Black hole researchers have tracked the orbits of stars, such as one called S2, circling this galactic drain for years. Should those stars be feeling the tug from distant doppelgängers beyond the black hole, they’d perform a very particular dance for anybody watching, according to a recent calculation.
“If astronomers just measure the orbit of S2 with higher precision so that we can narrow it down [and notice such a dance],” says Dejan Stojkovic, a theoretical physicist at the University at Buffalo who helped calculate the result, “that’s it. That’s huge.”
Wormholes represent one strange shape of space theoretically allowed under the auspices of Einstein’s theory of gravity, but only black holes have the oomph required to actually sculpt one. One way to check if a given black hole has managed to put a pleat in the fabric of space would be to pull an Interstellar and try to send a probe through, but we’d have to wait thousands of years for any spacecraft to reach the nearest candidates.
To make such a mission even more quixotic, most physicists agree that human-traversable, sci-fi-style bridges can’t exist. The only way to fight their natural tendency to collapse, according to Einstein’s equations, is to put in a type of repulsion that other laws of physics forbid on large scales—negative energy (physics students may remember that energy, unlike velocity or acceleration, always comes out positive). Stojkovic says he and his collaborators avoided such “hocus pocus” in their previous work, describing a wormhole that would work in our universe.
However, just because astronauts can’t travel through a large wormhole doesn’t mean that nothing can. Working within the framework of Einstein’s theory of gravity, in the previous work the group found a way to build a big, stable wormhole kept open by the force driving the expansion of the universe. The new work extends the old, calculating that while most particles and electric fields stopped short, the force of gravity can sail smoothly through. That means, theoretically, objects on our side could feel the tug of something especially massive on the other side. “We were kind of surprised,” Stojkovic says, “but what else would you expect? Gravity is the property of spacetime itself.”
The research, published in 2019 in the journal Physical Review D, goes on to ask whether astronomers could detect such subtle gravitational tugs on stars in the Milky Way.
The ideal target, Stojkovic and his colleagues propose, is Sagittarius (Sag) A—the black hole that allegedly sits at the heart of our galaxy. More specifically, they calculated the possible effects on S2, a star that orbits Sag A. If the black hole harbors a wormhole within it, similar stars would likely orbit on the other side, somewhere else in the universe, and S2 might feel the gravitational pull of a distant twin traveling through the cosmic connection between them.
Any resultant swerves S2 might make would be slight, but after more than 20 years of observation astronomers have clocked the star’s acceleration to four-decimal-place precision. With roughly 100 times more accuracy than that, Stojkovic estimates, astronomers would have the sensitivity to test his wormhole hypothesis—a benchmark he says current experiments should naturally reach in a couple more decades of data collection. If S2’s motion brings no surprises at that point, he says, then Sag A* must either be an everyday black hole, or a wormhole linking to a rather empty area of space.
But while Stojkovic and his colleagues analyzed their large wormhole using Einstein’s equations, other theorists studying the (as yet theoretical) microscopic properties of space and gravity aren’t so sure these conclusions hold at the particle level. Daniel Jafferis, a physicist at Harvard University, says that since no one has proposed a way for large wormholes to form, any odd jigs by S2 would raise more questions than they would answer. “Someone would probably have had to have made the wormhole intentionally,” he says. And the only thing less likely than a real wormhole might be a real wormhole constructed by super advanced aliens.
Furthermore, he suggests that the realities of particle physics may clash with conclusions drawn purely from Einstein’s equations, and that without the “magic” of negative energy, non-traversable really means non-traversable, full stop. “Nothing can get through, including gravitons [the hypothetical gravity particle],” Jafferis says. “So it seems [the wormhole] cannot be seen or detected from the outside.”
Stojkovic, who says he was motivated to do the calculation purely from personal curiosity, fully acknowledges the astronomically long odds. Nevertheless, since astronomers are collecting the data anyway, he loses nothing by waiting with an open mind. “If one worm hole is found, then there is no reason to believe that there aren’t many others,” he says. “When we found the first candidate for a black hole, then suddenly we saw millions of them.”
Charlie Wood is a journalist covering developments in the physical sciences both on and off the planet. In addition to Popular Science, his work has appeared in Quanta Magazine, Scientific American, The Christian Science Monitor, and other publications. Previously, he taught physics and English in Mozambique and Japan, and studied physics at Brown University.
February 9th 2023
Why More Physicists Are Starting to Think Space and Time Are ‘Illusions’
MINDBLOWN
A concept called “quantum entanglement” suggests the fabric of the universe is more interconnected than we think. And it also suggests we have the wrong idea about reality.
Heinrich Päs
Updated Jan. 30, 2023 11:39AM ET / Published Jan. 28, 2023 11:53PM ET

This past December, the physics Nobel Prize was awarded for the experimental confirmation of a quantum phenomenon known for more than 80 years: entanglement. As envisioned by Albert Einstein and his collaborators in 1935, quantum objects can be mysteriously correlated even if they are separated by large distances. But as weird as the phenomenon appears, why is such an old idea still worth the most prestigious prize in physics?
Coincidentally, just a few weeks before the new Nobel laureates were honored in Stockholm, a different team of distinguished scientists from Harvard, MIT, Caltech, Fermilab and Google reported that they had run a process on Google’s quantum computer that could be interpreted as a wormhole. Wormholes are tunnels through the universe that can work like a shortcut through space and time and are loved by science fiction fans, and although the tunnel realized in this recent experiment exists only in a 2-dimensional toy universe, it could constitute a breakthrough for future research at the forefront of physics.
But why is entanglement related to space and time? And how can it be important for future physics breakthroughs? Properly understood, entanglement implies that the universe is “monistic”, as philosophers call it, that on the most fundamental level, everything in the universe is part of a single, unified whole. It is a defining property of quantum mechanics that its underlying reality is described in terms of waves, and a monistic universe would require a universal function. Already decades ago, researchers such as Hugh Everett and Dieter Zeh showed how our daily-life reality can emerge out of such a universal quantum-mechanical description. But only now are researchers such as Leonard Susskind or Sean Carroll developing ideas on how this hidden quantum reality might explain not only matter but also the fabric of space and time.
Entanglement is much more than just another weird quantum phenomenon. It is the acting principle behind both why quantum mechanics merges the world into one and why we experience this fundamental unity as many separate objects. At the same time, entanglement is the reason why we seem to live in a classical reality. It is—quite literally—the glue and creator of worlds. Entanglement applies to objects comprising two or more components and describes what happens when the quantum principle that “everything that can happen actually happens” is applied to such composed objects. Accordingly, an entangled state is the superposition of all possible combinations that the components of a composed object can be in to produce the same overall result. It is again the wavy nature of the quantum domain that can help to illustrate how entanglement actually works.
Picture a perfectly calm, glassy sea on a windless day. Now ask yourself, how can such a plane be produced by overlaying two individual wave patterns? One possibility is that superimposing two completely flat surfaces results again in a completely level outcome. But another possibility that might produce a flat surface is if two identical wave patterns shifted by half an oscillation cycle were to be superimposed on one another, so that the wave crests of one pattern annihilate the wave troughs of the other one and vice versa. If we just observed the glassy ocean, regarding it as the result of two swells combined, there would be no way for us to find out about the patterns of the individual swells. What sounds perfectly ordinary when we talk about waves has the most bizarre consequences when applied to competing realities. If your neighbor told you she had two cats, one live cat and a dead one, this would imply that either the first cat or the second one is dead and that the remaining cat, respectively, is alive—it would be a strange and morbid way of describing one’s pets, and you may not know which one of them is the lucky one, but you would get the neighbor’s drift. Not so in the quantum world. In quantum mechanics, the very same statement implies that the two cats are merged in a superposition of cases, including the first cat being alive and the second one dead and the first cat being dead while the second one lives, but also possibilities where both cats are half alive and half dead, or the first cat is one-third alive, while the second feline adds the missing two-thirds of life. In a quantum pair of cats, the fates and conditions of the individual animals get dissolved entirely in the state of the whole. Likewise, in a quantum universe, there are no individual objects. All that exists is merged into a single “One.”
“I’m almost certain that space and time are illusions. These are primitive notions that will be replaced by something more sophisticated.”
— Nathan Seiberg, Institute for Advanced Study
Quantum entanglement reveals to us a vast and entirely new territory to explore. It defines a new foundation of science and turns our quest for a theory of everything upside down—to build on quantum cosmology rather than on particle physics or string theory. But how realistic is it for physicists to pursue such an approach? Surprisingly, it is not just realistic—they are actually doing it already. Researchers at the forefront of quantum gravity have started to rethink space-time as a consequence of entanglement. An increasing number of scientists have come to ground their research in the nonseparability of the universe. Hopes are high that by following this approach they may finally come to grasp what space and time, deep down at the foundation, really are.
Whether space is stitched together by entanglement, physics is described by abstract objects beyond space and time or the space of possibilities represented by Everett’s universal wave function, or everything in the universe is traced back to a single quantum object—all these ideas share a distinct monistic flavor. At present it is hard to judge which of these ideas will inform the future of physics and which will eventually disappear. What’s interesting is that while originally ideas were often developed in the context of string theory, they seem to have outgrown string theory, and strings play no role anymore in the most recent research. A common thread now seems to be that space and time are not considered fundamental anymore. Contemporary physics doesn’t start with space and time to continue with things placed in this preexisting background. Instead, space and time themselves are considered products of a more fundamental projector reality. Nathan Seiberg, a leading string theorist at the Institute for Advanced Study at Princeton, New Jersey, is not alone in his sentiment when he states, “I’m almost certain that space and time are illusions. These are primitive notions that will be replaced by something more sophisticated.” Moreover, in most scenarios proposing emergent space-times, entanglement plays the fundamental role. As philosopher of science Rasmus Jaksland points out, this eventually implies that there are no individual objects in the universe anymore; that everything is connected with everything else: “Adopting entanglement as the world making relation comes at the price of giving up separability. But those who are ready to take this step should perhaps look to entanglement for the fundamental relation with which to constitute this world (and perhaps all the other possible ones).” Thus, when space and time disappear, a unified One emerges.

Conversely, from the perspective of quantum monism, such mind-boggling consequences of quantum gravity are not far off. Already in Einstein’s theory of general relativity, space is no static stage anymore; rather it is sourced by matter’s masses and energy. Much like the German philosopher Gottfried W. Leibniz’s view, it describes the relative order of things. If now, according to quantum monism, there is only one thing left, there is nothing left to arrange or order and eventually no longer a need for the concept of space on this most fundamental level of description. It is “the One,” a single quantum universe that gives rise to space, time, and matter.
“GR=QM,” Leonard Susskind claimed boldly in an open letter to researchers in quantum information science: general relativity is nothing but quantum mechanics—a hundred-year-old theory that has been applied extremely successfully to all sorts of things but never really entirely understood. As Sean Carroll has pointed out, “Maybe it was a mistake to quantize gravity, and space-time was lurking in quantum mechanics all along.” For the future, “rather than quantizing gravity, maybe we should try to gravitize quantum mechanics. Or, more accurately but less evocatively, ‘find gravity inside quantum mechanics,’” Carroll suggests on his blog. Indeed, it seems that if quantum mechanics had been taken seriously from the beginning, if it had been understood as a theory that isn’t happening in space and time but within a more fundamental projector reality, many of the dead ends in the exploration of quantum gravity could have been avoided. If we had approved the monistic implications of quantum mechanics—the heritage of a three-thousand-year-old philosophy that was embraced in antiquity, persecuted in the Middle Ages, revived in the Renaissance, and tampered with in Romanticism—as early as Everett and Zeh had pointed them out rather than sticking to the influential quantum pioneer Niels Bohr’s pragmatic interpretation that reduced quantum mechanics to a tool, we would be further on the way to demystifying the foundations of reality.
Adapted from The One: How an Ancient Idea Holds the Future of Physics by Heinrich Päs. Copyright © 2023. Available from Basic Books, an imprint of Hachette Book Group, Inc.
February 8th 2023
Quantum breakthrough could revolutionise computing
By Pallab Ghosh
Science correspondent
Scientists have come a step closer to making multi-tasking ‘quantum’ computers, far more powerful than even today’s most advanced supercomputers.
Quantum computers make use of the weird qualities of sub-atomic particles.
So-called quantum particles can be in two places at the same time and also strangely connected even though they are millions of miles apart.
A Sussex University team transferred quantum information between computer chips at record speeds and accuracy.

Computer scientists have been trying to make an effective quantum computer for more than 20 years. Firms such as Google, IBM and Microsoft have developed simple machines. But, according to Prof Winfried Hensinger, who led the research at Sussex University, the new development paves the way for systems that can solve complex real world problems that the best computers we have today are incapable of.
“Right now we have quantum computers with very simple microchips,” he said. “What we have achieved here is the ability to realise extremely powerful quantum computers capable of solving some of the most important problems for industries and society.”

Currently, computers solve problems in a simple linear way, one calculation at a time.
In the quantum realm, particles can be in two places at the same time and researchers want to harness this property to develop computers that can do multiple calculations all at the same time.
Quantum particles can also be millions of miles apart and be strangely connected, mirroring each other’s actions instantaneously. Again, that could also be used to develop much more powerful computers.

One stumbling block has been the need to transfer quantum information between chips quickly and reliably: the information degrades, and errors are introduced.
But Prof Hensinger’s team has made a breakthrough, published in the journal Nature Communications, which may have overcome that obstacle.
The team developed a system able to transport information from one chip to another with a reliability of 99.999993% at record speeds. That, say the researchers, shows that in principle chips could be slotted together to make a more powerful quantum computer.

Prof Michael Cuthbert, who is the director of the newly established National Quantum Computing Centre in Didcot, Oxfordshire and is independent of the Sussex research group described the development as a “really important enabling step”. But he said that more work was needed to develop practical systems.
“To build the type of quantum computer you need in the future, you start off by connecting chips that are the size of your thumbnail until you get something the size of a dinner plate. The Sussex group has shown you can have the stability and speed for that step.
“But then you need a mechanism to connect these dinner plates together to scale up a machine, potentially as large as a football pitch, in order to carry out realistic and useful computations, and the technology for communications for that scale is not yet available.”
PhD student Sahra Kulmiya, who carried out the Sussex experiment, says that the team are ready for the challenge to take the technology to the next level.
“It is not just solely a physics problem anymore,” she told BBC News.
“It is an engineering problem, a computer science problem and also a mathematical problem.
“It is really difficult to say how close we are to the realisation of quantum computing, but I’m optimistic in how it can become relevant to us in our everyday lives.”
One of the UK’s leading engineering firms, Rolls Royce, is also optimistic about the technology. It is working with the Sussex researchers to develop machines that could help them design even better jet engines.
Powerful supercomputers are used to model the flow of air in simulations to test out new designs of aircraft engines.
Transforming engineering
A quantum computer could in principle track the airflow with even greater accuracy, and do so really quickly, according to Prof Leigh Lapworth, who is leading the development of quantum computing for Rolls-Royce.
“Quantum computers would be able to do calculations that we can’t currently do and others that would take many months or years. The potential of doing those in days would just transform our design systems and lead to even better engines.”
The technology could potentially also be used to design drugs more quickly by accurately simulating their chemical reactions, a calculation too difficult for current supercomputers. They could also provide even more accurate systems to forecast weather and project the impact of climate change.
Prof Hensinger said he first had the idea of developing a quantum computer more than 20 years ago.
“People rolled their eyes and said: ‘it’s impossible’.”
“And when people tell me something can’t be done, I just love to try. So I have spent the past 20 years removing the barriers one by one to a point where one can now really build a practical quantum computer.”
| Something amazing every day.SIGN UP ⋅ WEBSITE |
| Artemis 1: Return to the Moon NASA’s Artemis 1 Orion spacecraft arrives in Florida (NASA’s Kennedy Space Center via Twitter) Orion made it to NASA’s Kennedy Space Center on Dec. 30. Full Story: Space (1/3) The Launchpad HAARP antenna array looks inside a passing asteroid (Wikimedia Commons) Some people think HAARP was built to trigger natural disasters, but it may, in fact, help to save Earth one day. Full Story: Space (1/4) Hubble sees ancient globular cluster near Milky Way’s heart (NASA, ESA and R. Cohen (Rutgers the State University of New Jersey); Processing: Gladys Kober (NASA/Catholic University of America)) The cluster is estimated to be about 12 billion years old. Full Story: Space (1/4) POLL QUESTION:Space quiz! The HAARP antenna array in Alaska recently used radio waves to try and peer inside a passing asteroid. What does HAARP stand for?Learn the answer here! High-frequency Active Auroral Research Program High-Altitude Astronomy Radio Program Helio-Atmospheric Alaskan Research Project High-energy Atmospheric Astronomy Radio Propagation |
Comment I very much regret abandoning maths , phyics and engineering for the pretentious highly dangerous politicised world of humanities where reason and logic are the last thing you require. My inner nerd makes me a natural target for the police state that strives to dicate truth. Sadly it also seeks to contain science. R J COOK
January 28th 2023
Quantum Leaps, Long Assumed to Be Instantaneous, Take Time
An experiment caught a quantum system in the middle of a jump — something the originators of quantum mechanics assumed was impossible.
Read when you’ve got time to spare.
Advertisement
More from Quanta Magazine
- Wormholes Reveal a Way to Manipulate Black Hole Information in the Lab
- How Big Can the Quantum World Be? Physicists Probe the Limits.
- Famous Experiment Dooms Pilot-Wave Alternative to Quantum Weirdness
Advertisement

A quantum leap is a rapidly gradual process. Credit: Quanta Magazine; source: qoncha.
When quantum mechanics was first developed a century ago as a theory for understanding the atomic-scale world, one of its key concepts was so radical, bold and counter-intuitive that it passed into popular language: the “quantum leap.” Purists might object that the common habit of applying this term to a big change misses the point that jumps between two quantum states are typically tiny, which is precisely why they weren’t noticed sooner. But the real point is that they’re sudden. So sudden, in fact, that many of the pioneers of quantum mechanics assumed they were instantaneous.
A 2019 experiment shows that they aren’t. By making a kind of high-speed movie of a quantum leap, the work reveals that the process is as gradual as the melting of a snowman in the sun. “If we can measure a quantum jump fast and efficiently enough,” said Michel Devoret of Yale University, “it is actually a continuous process.” The study, which was led by Zlatko Minev, a graduate student in Devoret’s lab, was published on Monday in Nature. Already, colleagues are excited. “This is really a fantastic experiment,” said the physicist William Oliver of the Massachusetts Institute of Technology, who wasn’t involved in the work. “Really amazing.”
But there’s more. With their high-speed monitoring system, the researchers could spot when a quantum jump was about to appear, “catch” it halfway through, and reverse it, sending the system back to the state in which it started. In this way, what seemed to the quantum pioneers to be unavoidable randomness in the physical world is now shown to be amenable to control. We can take charge of the quantum.
All Too Random
The abruptness of quantum jumps was a central pillar of the way quantum theory was formulated by Niels Bohr, Werner Heisenberg and their colleagues in the mid-1920s, in a picture now commonly called the Copenhagen interpretation. Bohr had argued earlier that the energy states of electrons in atoms are “quantized”: Only certain energies are available to them, while all those in between are forbidden. He proposed that electrons change their energy by absorbing or emitting quantum particles of light — photons — that have energies matching the gap between permitted electron states. This explained why atoms and molecules absorb and emit very characteristic wavelengths of light — why many copper salts are blue, say, and sodium lamps yellow.
Bohr and Heisenberg began to develop a mathematical theory of these quantum phenomena in the 1920s. Heisenberg’s quantum mechanics enumerated all the allowed quantum states, and implicitly assumed that jumps between them are instant — discontinuous, as mathematicians would say. “The notion of instantaneous quantum jumps … became a foundational notion in the Copenhagen interpretation,” historian of science Mara Beller has written.
Another of the architects of quantum mechanics, the Austrian physicist Erwin Schrödinger, hated that idea. He devised what seemed at first to be an alternative to Heisenberg’s math of discrete quantum states and instant jumps between them. Schrödinger’s theory represented quantum particles in terms of wavelike entities called wave functions, which changed only smoothly and continuously over time, like gentle undulations on the open sea. Things in the real world don’t switch suddenly, in zero time, Schrödinger thought — discontinuous “quantum jumps” were just a figment of the mind. In a 1952 paper called “Are there quantum jumps?,” Schrödinger answered with a firm “no,” his irritation all too evident in the way he called them “quantum jerks.”
The argument wasn’t just about Schrödinger’s discomfort with sudden change. The problem with a quantum jump was also that it was said to just happen at a random moment — with nothing to say why that particular moment. It was thus an effect without a cause, an instance of apparent randomness inserted into the heart of nature. Schrödinger and his close friend Albert Einstein could not accept that chance and unpredictability reigned at the most fundamental level of reality. According to the German physicist Max Born, the whole controversy was therefore “not so much an internal matter of physics, as one of its relation to philosophy and human knowledge in general.” In other words, there’s a lot riding on the reality (or not) of quantum jumps.
Seeing Without Looking
To probe further, we need to see quantum jumps one at a time. In 1986, three teams of researchers reported them happening in individual atoms suspended in space by electromagnetic fields. The atoms flipped between a “bright” state, where they could emit a photon of light, and a “dark” state that did not emit at random moments, remaining in one state or the other for periods of between a few tenths of a second and a few seconds before jumping again. Since then, such jumps have been seen in various systems, ranging from photons switching between quantum states to atoms in solid materials jumping between quantized magnetic states. In 2007 a team in France reported jumps that correspond to what they called “the birth, life and death of individual photons.”
In these experiments the jumps indeed looked abrupt and random — there was no telling, as the quantum system was monitored, when they would happen, nor any detailed picture of what a jump looked like. The Yale team’s setup, by contrast, allowed them to anticipate when a jump was coming, then zoom in close to examine it. The key to the experiment is the ability to collect just about all of the available information about it, so that none leaks away into the environment before it can be measured. Only then can they follow single jumps in such detail.
The quantum systems the researchers used are much larger than atoms, consisting of wires made from a superconducting material — sometimes called “artificial atoms” because they have discrete quantum energy states analogous to the electron states in real atoms. Jumps between the energy states can be induced by absorbing or emitting a photon, just as they are for electrons in atoms.
Devoret and colleagues wanted to watch a single artificial atom jump between its lowest-energy (ground) state and an energetically excited state. But they couldn’t monitor that transition directly, because making a measurement on a quantum system destroys the coherence of the wave function — its smooth wavelike behavior — on which quantum behavior depends. To watch the quantum jump, the researchers had to retain this coherence. Otherwise they’d “collapse” the wave function, which would place the artificial atom in one state or the other. This is the problem famously exemplified by Schrödinger’s cat, which is allegedly placed in a coherent quantum “superposition” of live and dead states but becomes only one or the other when observed.
To get around this problem, Devoret and colleagues employ a clever trick involving a second excited state. The system can reach this second state from the ground state by absorbing a photon of a different energy. The researchers probe the system in a way that only ever tells them whether the system is in this second “bright” state, so named because it’s the one that can be seen. The state to and from which the researchers are actually looking for quantum jumps is, meanwhile, the “dark” state — because it remains hidden from direct view.
The researchers placed the superconducting circuit in an optical cavity (a chamber in which photons of the right wavelength can bounce around) so that, if the system is in the bright state, the way that light scatters in the cavity changes. Every time the bright state decays by emission of a photon, the detector gives off a signal akin to a Geiger counter’s “click.”
The key here, said Oliver, is that the measurement provides information about the state of the system without interrogating that state directly. In effect, it asks whether the system is in, or is not in, the ground and dark states collectively. That ambiguity is crucial for maintaining quantum coherence during a jump between these two states. In this respect, said Oliver, the scheme that the Yale team has used is closely related to those employed for error correction in quantum computers. There, too, it’s necessary to get information about quantum bits without destroying the coherence on which the quantum computation relies. Again, this is done by not looking directly at the quantum bit in question but probing an auxiliary state coupled to it.
The strategy reveals that quantum measurement is not about the physical perturbation induced by the probe but about what you know (and what you leave unknown) as a result. “Absence of an event can bring as much information as its presence,” said Devoret. He compares it to the Sherlock Holmes story in which the detective infers a vital clue from the “curious incident” in which a dog did not do anything in the night. Borrowing from a different (but often confused) dog-related Holmes story, Devoret calls it “Baskerville’s Hound meets Schrödinger’s Cat.”
To Catch a Jump
The Yale team saw a series of clicks from the detector, each signifying a decay of the bright state, arriving typically every few microseconds. This stream of clicks was interrupted approximately every few hundred microseconds, apparently at random, by a hiatus in which there were no clicks. Then after a period of typically 100 microseconds or so, the clicks resumed. During that silent time, the system had presumably undergone a transition to the dark state, since that’s the only thing that can prevent flipping back and forth between the ground and bright states.
So here in these switches from “click” to “no-click” states are the individual quantum jumps — just like those seen in the earlier experiments on trapped atoms and the like. However, in this case Devoret and colleagues could see something new.
Before each jump to the dark state, there would typically be a short spell where the clicks seemed suspended: a pause that acted as a harbinger of the impending jump. “As soon as the length of a no-click period significantly exceeds the typical time between two clicks, you have a pretty good warning that the jump is about to occur,” said Devoret.
That warning allowed the researchers to study the jump in greater detail. When they saw this brief pause, they switched off the input of photons driving the transitions. Surprisingly, the transition to the dark state still happened even without photons driving it — it is as if, by the time the brief pause sets in, the fate is already fixed. So although the jump itself comes at a random time, there is also something deterministic in its approach.
With the photons turned off, the researchers zoomed in on the jump with fine-grained time resolution to see it unfold. Does it happen instantaneously — the sudden quantum jump of Bohr and Heisenberg? Or does it happen smoothly, as Schrödinger insisted it must? And if so, how?
The team found that jumps are in fact gradual. That’s because, even though a direct observation could reveal the system only as being in one state or another, during a quantum jump the system is in a superposition, or mixture, of these two end states. As the jump progresses, a direct measurement would be increasingly likely to yield the final rather than the initial state. It’s a bit like the way our decisions may evolve over time. You can only either stay at a party or leave it — it’s a binary choice — but as the evening wears on and you get tired, the question “Are you staying or leaving?” becomes increasingly likely to get the answer “I’m leaving.”
The techniques developed by the Yale team reveal the changing mindset of a system during a quantum jump. Using a method called tomographic reconstruction, the researchers could figure out the relative weightings of the dark and ground states in the superposition. They saw these weights change gradually over a period of a few microseconds. That’s pretty fast, but it’s certainly not instantaneous.
What’s more, this electronic system is so fast that the researchers could “catch” the switch between the two states as it is happening, then reverse it by sending a pulse of photons into the cavity to boost the system back to the dark state. They can persuade the system to change its mind and stay at the party after all.
Flash of Insight
The experiment shows that quantum jumps “are indeed not instantaneous if we look closely enough,” said Oliver, “but are coherent processes”: real physical events that unfold over time.
The gradualness of the “jump” is just what is predicted by a form of quantum theory called quantum trajectories theory, which can describe individual events like this. “It is reassuring that the theory matches perfectly with what is seen” said David DiVincenzo, an expert in quantum information at Aachen University in Germany, “but it’s a subtle theory, and we are far from having gotten our heads completely around it.”
The possibility of predicting quantum jumps just before they occur, said Devoret, makes them somewhat like volcanic eruptions. Each eruption happens unpredictably, but some big ones can be anticipated by watching for the atypically quiet period that precedes them. “To the best of our knowledge, this precursory signal [to a quantum jump] has not been proposed or measured before,” he said.
Devoret said that an ability to spot precursors to quantum jumps might find applications in quantum sensing technologies. For example, “in atomic clock measurements, one wants to synchronize the clock to the transition frequency of an atom, which serves as a reference,” he said. But if you can detect right at the start if the transition is about to happen, rather than having to wait for it to be completed, the synchronization can be faster and therefore more precise in the long run.
DiVincenzo thinks that the work might also find applications in error correction for quantum computing, although he sees that as “quite far down the line.” To achieve the level of control needed for dealing with such errors, though, will require this kind of exhaustive harvesting of measurement data — rather like the data-intensive situation in particle physics, said DiVincenzo.
The real value of the result is not, though, in any practical benefits; it’s a matter of what we learn about the workings of the quantum world. Yes, it is shot through with randomness — but no, it is not punctuated by instantaneous jerks. Schrödinger, aptly enough, was both right and wrong at the same time.
Philip Ball is a science writer and author based in London who contributes frequently to Nature, New Scientist, Prospect, Nautilus and The Atlantic, among other publications.
- Philip Ball
January 14th 2023
The Remarkable Emptiness of Existence
Early scientists didn’t know it, but we do now: The void in the universe is alive.
- By Paul M. Sutter
- January 4, 2023

In 1654 a German scientist and politician named Otto von Guericke was supposed to be busy being the mayor of Magdeburg. But instead he was putting on a demonstration for lords of the Holy Roman Empire. With his newfangled invention, a vacuum pump, he sucked the air out of a copper sphere constructed of two hemispheres. He then had two teams of horses, 15 in each, attempt to pull the hemispheres apart. To the astonishment of the royal onlookers, the horses couldn’t separate the hemispheres because of the overwhelming pressure of the atmosphere around them.
Von Guericke became obsessed by the idea of a vacuum after learning about the recent and radical idea of a heliocentric universe: a cosmos with the sun at the center and the planets whipping around it. But for this idea to work, the space between the planets had to be filled with nothing. Otherwise friction would slow the planets down.
The vacuum is singing to us, a harmony underlying reality itself.
Scientists, philosophers, and theologians across the globe had debated the existence of the vacuum for millennia, and here was von Guericke and a bunch of horses showing that it was real. But the idea of the vacuum remained uncomfortable, and only begrudgingly acknowledged. We might be able to artificially create a vacuum with enough cleverness here on Earth, but nature abhorred the idea. Scientists produced a compromise: The space of space was filled with a fifth element, an aether, a substance that did not have much in the way of manifest properties, but it most definitely wasn’t nothing.
But as the quantum and cosmological revolutions of the 20th century arrived, scientists never found this aether and continued to turn up empty handed.
The more we looked, through increasingly powerful telescopes and microscopes, the more we discovered nothing. In the 1920s astronomer Edwin Hubble discovered that the Andromeda nebula was actually the Andromeda galaxy, an island home of billions of stars sitting a staggering 2.5 million light-years away. As far as we could tell, all those lonely light-years were filled with not much at all, just the occasional lost hydrogen atom or wandering photon. Compared to the relatively small size of galaxies themselves (our own Milky Way stretches across for a mere 100,000 light-years), the universe seemed dominated by absence.
At subatomic scales, scientists were also discovering atoms to be surprisingly empty places. If you were to rescale a hydrogen atom so that its nucleus was the size of a basketball, the nearest electron would sit around two miles away. With not so much as a lonely subatomic tumbleweed in between.

Nothing. Absolutely nothing. Continued experiments and observations only served to confirm that at scales both large and small, we appeared to live in an empty world.
And then that nothingness cracked open. Within the emptiness that dominates the volume of an atom and the volume of the universe, physicists found something. Far from the sedate aether of yore, this something is strong enough to be tearing our universe apart. The void, it turns out, is alive.
In December 2022, an international team of astronomers released the results of their latest survey of galaxies, and their work has confirmed that the vacuum of spacetime is wreaking havoc across the cosmos. They found that matter makes up only a minority contribution to the energy budget of the universe. Instead, most of the energy within the cosmos is contained in the vacuum, and that energy is dominating the future evolution of the universe.
Their work is the latest in a string of discoveries stretching back over two decades. In the late 1990s, two independent teams of astronomers discovered that the expansion of the universe is accelerating, meaning that our universe grows larger and larger faster and faster every day. The exact present-day expansion rate is still a matter of some debate among cosmologists, but the reality is clear: Something is making the universe blow up. It appears as a repulsive gravitational force, and we’ve named it dark energy.
The trick here is that the vacuum, first demonstrated by von Guericke all those centuries ago, is not as empty as it seems. If you were to take a box (or, following von Guericke’s example, two hemispheres), and remove everything from it, including all the particles, all the light, all the everything, you would not be left with, strictly speaking, nothing. What you’d be left with is the vacuum of spacetime itself, which we’ve learned is an entity in its own right.
Nothing contains all things. It is more precious than gold.
We live in a quantum universe; a universe where you can never be quite sure about anything. At the tiniest of scales, subatomic particles fizz and pop into existence, briefly experiencing the world of the living before returning back from where they came, disappearing from reality before they have a chance to meaningfully interact with anything else.
This phenomenon has various names: the quantum foam, the spacetime foam, vacuum fluctuations. This foam represents a fundamental energy to the vacuum of spacetime itself, a bare ground level on which all other physical interactions take place. In the language of quantum field theory, the offspring of the marriage of quantum mechanics and special relativity, quantum fields representing every kind of particle soak the vacuum of spacetime like crusty bread dipped in oil and vinegar. Those fields can’t help but vibrate at a fundamental, quantum level. In this view, the vacuum is singing to us, a harmony underlying reality itself.
In our most advanced quantum theories, we can calculate the energy contained in the vacuum, and it’s infinite. As in, suffusing every cubic centimeter of space and time is an infinite amount of energy, the combined efforts of all those countless but effervescent particles. This isn’t necessarily a problem for the physics that we’re used to, because all the interactions of everyday experience sit “on top of” (for lack of a better term) that infinite tower of energy—it just makes the math a real pain to work with.
All this would be mathematically annoying but otherwise unremarkable except for the fact that in Einstein’s general theory of relativity, vacuum energy has the curious ability to generate a repulsive gravitational force. We typically never notice such effects because the vacuum energy is swamped by all the normal mass within it (in von Guericke’s case, the atmospheric pressure surrounding his hemispheres was the dominant force at play). But at the largest scales there’s so much raw nothingnessto the universe that these effects become manifest as an accelerated expansion. Recent research suggests that around 5 billion years ago, the matter in the universe diluted to the point that dark energy could come to the fore. Today, it represents roughly 70 percent of the entire energy budget of the cosmos. Studies have shown that dark energy is presently in the act of ripping apart the large-scale structure of the universe, tearing apart superclusters of galaxies and disentangling the cosmic web before our eyes.
But the acceleration isn’t all that rapid. When we calculate how much vacuum energy is needed to create the dark energy effect, we only get a small number.
But our quantum understanding of vacuum energy says it should be infinite, or at least incredibly large. Definitely not small. This discrepancy between the theoretical energy of the vacuum and the observed value is one of the greatest mysteries in modern physics. And it leads to the question about what else might be lurking in the vast nothingness of our atoms and our universe. Perhaps von Guericke was right all along. “Nothing contains all things,” he wrote. “It is more precious than gold, without beginning and end, more joyous than the perception of bountiful light, more noble than the blood of kings, comparable to the heavens, higher than the stars, more powerful than a stroke of lightening, perfect and blessed in every way.” ![]()
Paul M. Sutter is a research professor in astrophysics at the Institute for Advanced Computational Science at Stony Brook University and a guest researcher at the Flatiron Institute in New York City. He is the author of Your Place in the Universe: Understanding our Big, Messy Existence.
Lead image: ANON MUENPROM / Shutterstock
Get the Nautilus newsletter
The newest and most popular articles delivered right to your inbox! Newsletter Signup (Embedded) If you are human, leave this field blank.
Should People Live on the Moon?
One question for Joseph Silk, an astrophysicist at Johns Hopkins University.
- By Brian Gallagher
- January 9, 2023
- Share


One question for Joseph Silk, an astrophysicist at Johns Hopkins University and the author of Back to the Moon: The Next Giant Leap for Humankind.

Should people live on the moon?
Why not? We have to start somewhere if we ever want to leave Earth. And the only realistic place to start is the moon. It’s going to be for a minority, right? For explorers, for people exploiting the moon for commercial reasons, for scientists. They will be living on the moon within the next century. And it will be a starting point to go elsewhere. It’s a much easier environment, because of the low gravity, from which to send spacecraft farther afield.
If your interest is commercial, then you’ll probably focus on mining because we’re running out of certain rare-earth elements on Earth critical for our computer industry. There’s a hugely abundant supply on the moon, thanks to its history of bombardment by meteorites throughout billions of years. Beyond that there’s tourism. You can already buy tickets—not cheap, of course—for a trip around the moon, perhaps in the next five years, because of people like Elon Musk. The moon’s also got a huge abundance—this is not very widely known—of water ice. Inside deep, dark craters. Not only does that help you have a major resource for life, but maybe the most important use of water will be to break it down into oxygen, hydrogen. Liquefy these—you have abundant power from the sun to do this—and lo and behold, you have rocket fuel to take you throughout the inner solar system and beyond.
I’m very attracted to the moon as a place to build telescopes. We can see stars really sharply, with no obscuration. Water vapor in Earth’s atmosphere masks out much of the infrared light from the stars where there’s huge amounts of information about what the stars are made of. Also, because of our ionosphere, Earth is a very difficult place to receive low-frequency radio waves in space. These are inaccessible from Earth because we’ll be looking deep into the universe, where the wavelengths of these waves get stretched out by the expansion of the universe. Earth’s ionosphere distorts them. So, on the moon, we can view the universe as we never could before in radio waves.
A giant lava tube is large enough to house an entire city.
The only way to capture these really faint things is with a huge telescope. The James Webb is a small telescope—six meters. The far side of the moon is a unique place for doing that, and there are some futuristic schemes now to build a mega telescope inside a crater, a natural bowl. You can line the inside of that bowl with a number of small telescopes, maybe hundreds of them, and they would operate coherently, supported by wires from the crater edges. The size of the telescope determines how much light you can collect. You could have hundreds of times more light-gathering power on the moon.
Suddenly you have a telescope that’s kilometers across, and this would be the most amazing thing I could imagine, because then you could have not just light-collecting power, but resolving power. You could actually directly image the nearest exoplanets and look to see: “Do they have oceans? Do they have forests?” The first things you want to look for, if you want to explore the possibilities of distant, alien life. I’m rather doubtful that we’ll find life in our solar system. We have to look much farther away. Many light-years away. And that we can do with these giant telescopes.
The people working on the moon will have to figure out how to make a biosphere. Could be inside an artificial construction on the lunar surface. But that will not be very large. A much more promising approach, again in the next decades, will be to use a giant lava tube. These are huge, natural caves, relics of ancient volcanic activity. A giant lava tube is large enough to house an entire city. You can imagine air proofing that and developing a local atmosphere inside that, which would be a great place to live and certainly do new things on the moon. Things you would never do on Earth.
That is my most optimistic scenario for having large numbers of people. By no means millions, but maybe thousands of people living and working on the moon. One has to be optimistic that the international community will recognize that cooperation is the only way to go in the future, and establish lunar law that will control both real estate and also, I imagine, crime activity, if people start disputing territories. I’m hoping we have a legal framework. Right now, we seem very far away from this, but it’s got to happen. We have maybe one or two decades before the moon becomes a competitive place and exploration heats up. ![]()
Lead image: Nostalgia for Infinity / Shutterstock
- Brian GallagherPosted on January 9, 2023 Brian Gallagher is an associate editor at Nautilus. Follow him on Twitter @bsgallagher.
Get the Nautilus newsletter
The newest and most popular articles delivered right to your inbox!
January 9th 2023
Study Shows How The Universe Would Look if You Broke The Speed of Light, And It’s Weird
Physics02 January 2023
By David Nield
 (Omar Jabri/EyeEm/Getty Images)
(Omar Jabri/EyeEm/Getty Images)
Nothing can go faster than light. It’s a rule of physics woven into the very fabric of Einstein’s special theory of relativity. The faster something goes, the closer it gets to its perspective of time freezing to a standstill.
Go faster still, and you run into issues of time reversing, messing with notions of causality.
But researchers from the University of Warsaw in Poland and the National University of Singapore have now pushed the limits of relativity to come up with a system that doesn’t run afoul of existing physics, and might even point the way to new theories.
What they’ve come up with is an “extension of special relativity” that combines three time dimensions with a single space dimension (“1+3 space-time”), as opposed to the three spatial dimensions and one time dimension that we’re all used to.
Rather than creating any major logical inconsistencies, this new study adds more evidence to back up the idea that objects might well be able to go faster than light without completely breaking our current laws of physics.
“There is no fundamental reason why observers moving in relation to the described physical systems with speeds greater than the speed of light should not be subject to it,” says physicist Andrzej Dragan, from the University of Warsaw in Poland.
This new study builds on previous work by some of the same researchers which posits that superluminal perspectives could help tie together quantum mechanics with Einstein’s special theory of relativity – two branches of physics that currently can’t be reconciled into a single overarching theory that describes gravity in the same way we explain other forces.
Particles can no longer be modelled as point-like objects under this framework, as we might in the more mundane 3D (plus time) perspective of the Universe.
Instead, to make sense of what observers might see and how a superluminal particle might behave, we’d need to turn to the kinds of field theories that underpin quantum physics.
Based on this new model, superluminal objects would look like a particle expanding like a bubble through space – not unlike a wave through a field. The high-speed object, on the other hand, would ‘experience’ several different timelines.
Even so, the speed of light in a vacuum would remain constant even for those observers going faster than it, which preserves one of Einstein’s fundamental principles – a principle that has previously only been thought about in relation to observers going slower than the speed of light (like all of us).
“This new definition preserves Einstein’s postulate of constancy of the speed of light in vacuum even for superluminal observers,” says Dragan.
“Therefore, our extended special relativity does not seem like a particularly extravagant idea.”
However, the researchers acknowledge that switching to a 1+3 space-time model does raise some new questions, even while it answers others. They suggest that extending the theory of special relativity to incorporate faster-than-light frames of reference is needed.
That may well involve borrowing from quantum field theory: a combination of concepts from special relativity, quantum mechanics, and classical field theory (which aims to predict how physical fields are going to interact with each other).
If the physicists are right, the particles of the Universe would all have extraordinary properties in extended special relativity.
One of the questions raised by the research is whether or not we would ever be able to observe this extended behavior – but answering that is going to require a lot more time and a lot more scientists.
“The mere experimental discovery of a new fundamental particle is a feat worthy of the Nobel Prize and feasible in a large research team using the latest experimental techniques,” says physicist Krzysztof Turzyński, from the University of Warsaw.
“However, we hope to apply our results to a better understanding of the phenomenon of spontaneous symmetry breaking associated with the mass of the Higgs particle and other particles in the Standard Model, especially in the early Universe.”
The research has been published in Classical and Quantum Gravity.
Trending News
Something Strange Happens to The Temperature Around Freshly Formed Bubbles Physics3 days ago
We May Finally Know Why Some People Don’t Recover Their Sense of Smell After COVID Health3 days ago
The Chilling Tale of The ‘Demon Core’ And The Scientists Who Became Its Victims Humans4 days ago
January 7th 2023
We’ve Never Found Anything Like The Solar System. Is It a Freak in Space?
Space29 December 2022
Since the landmark discovery in 1992 of two planets orbiting a star outside of our Solar System, thousands of new worlds have been added to a rapidly growing list of ‘exoplanets’ in the Milky Way galaxy.
We’ve learnt many things from this vast catalogue of alien worlds orbiting alien stars. But one small detail stands out like a sore thumb. We’ve found nothing else out there like our own Solar System.
This has led some to conclude that our home star and its brood could be outliers in some way – perhaps the only planetary system of its kind.
By extension, this could mean life itself is an outlier; that the conditions that formed Earth and its veneer of self-replicating chemistry are difficult to replicate.
If you’re just looking at the numbers, the outlook is grim. By a large margin, the most numerous exoplanets we’ve identified to date are of a type not known to be conducive to life: giants and subgiants, of the gas and maybe ice variety.
Most exoplanets we’ve seen so far orbit their stars very closely, practically hugging them; so close that their sizzling temperatures would be much higher than the known habitability range.

It’s possible that as we continue searching, the statistics will balance out and we’ll see more places that remind us of our own backyard. But the issue is much more complex than just looking at numbers. Exoplanet science is limited by the capabilities of our technology. More than that, our impression of the true variety of alien worlds risks being limited by our own imagination.
What’s really out there in the Milky Way galaxy, and beyond, may be very different from what we actually see.
Expectations, and how to thwart them
Exoplanet science has a history of subverting expectations, right from the very beginning.
“If you go back to that world I grew up in when I was a kid, we only knew of one planetary system,” planetary scientist Jonti Horner of the University of Southern Queensland tells ScienceAlert.
“And so that was this kind of implicit assumption, and sometimes the explicit assumption, that all planetary systems would be like this. You know, you’d have rocky planets near the star that were quite small, you’d have gas giants a long way from the star that were quite big. And that’s how planetary systems would be.”
For this reason, it took scientists a while to identify an exoplanet orbiting a main sequence star, like our Sun. Assuming other solar systems were like ours, the tell-tale signs of heavyweight planets tugging on their stars would take years to observe, just as it takes our own gas giants years to complete an orbit.
Based on such lengthy periods of a single measurement, it didn’t seem worth the trouble to sift through a relatively short history of observations for many stars to conclusively sift out a fellow main-sequence solar system.
When they finally did look, the exoplanet they found was nothing like what they were expecting: a gas giant half the mass (and twice the size) of Jupiter orbiting so close to its host star, its year equals 4.2 days, and its atmosphere scorches at temperatures of around 1,000 degrees Celsius (1800 degrees Fahrenheit).
Since then, we’ve learnt these ‘Hot Jupiter’ type planets aren’t oddities at all. If anything, they seem relatively common.
We know now that there’s a lot more variety out there in the galaxy than what we see in our home system. However, it’s important not to assume that what we can currently detect is all that the Milky Way has to offer. If there’s anything out there like our own Solar System, it’s very possibly beyond our detection capabilities.
“Things like the Solar System are very hard for us to find, they’re a bit beyond us technologically at the minute,” Horner says.
“The terrestrial planets would be very unlikely to be picked up from any of the surveys we’ve done so far. You’re very unlikely to be able to find a Mercury, Venus, Earth and Mars around a star like the Sun.”
How to find a planet
Let’s be perfectly clear: the methods we use to detect exoplanets are incredibly clever. There are currently two that are the workhorses of the exoplanet detection toolkit: the transit method, and the radial velocity method.
In both cases, you need a telescope sensitive to very minute changes in the light of a star. The signals each are looking for, however, couldn’t be more different.
For the transit method you’ll need a telescope that can keep a star fixed in its view for a sustained period of time. That’s why instruments such as NASA’s space-based Transiting Exoplanet Survey Satellite (TESS) is such a powerhouse, capable of locking onto a segment of the sky for over 27 days without being interrupted by Earth’s rotation.
Invading astronomy one exoplanet gif at a time! This time with a gif showing the transit method for detecting exoplanets 😊 pic.twitter.com/2ZHv24DRTH— Alysa Obertas (parody) (@AstroAlysa) September 1, 2021
The aim for these kinds of telescopes is to spot the signal of a transit – when an exoplanet passes between us and its host star, like a tiny cloud blotting out a few rays of sunshine. These dips in light are tiny, as you can imagine. And one blip is insufficient to confidently infer the presence of an exoplanet; there are many things that can dim a star’s light, many of which are one-off events. Multiple transits, especially ones that exhibit regular periodicity, are the gold standard.
Therefore, larger exoplanets that are on short orbital periods, closer to their stars than Mercury is to the Sun (some much, much closer, on orbits of less than one Earth week), are favored in the data.
In case you missed it, my gif showing how exoplanets are detected via the radial velocity method is now available in dark mode! pic.twitter.com/P4yvXQVSUt— Alysa Obertas (parody) (@AstroAlysa) August 15, 2022
The radial velocity method detects the wobble of a star caused by the gravitational pull of the exoplanet as it swings around in its orbit. A planetary system, you see, doesn’t really orbit a star, so much as dance in a coordinated shuffle. The star and the planets orbit a mutual center of gravity, known as the barycenter. For the Solar System, that’s a point very, very close to the surface of the Sun, or just outside it, primarily due to the influence of Jupiter, which is more than twice the mass of all the rest of the planets combined.
Unlike a transit’s blink-and-you-miss-it event, the shift in the star’s position is an ongoing change that doesn’t require constant monitoring to notice. We can detect the motion of distant stars orbiting their barycenters because that motion changes their light due to something called the Doppler effect.
As the star moves towards us, the waves of light coming in our direction are squished slightly, towards the bluer end of the spectrum; as it moves away, the waves stretch towards the redder end. A regular ‘wobble’ in the star’s light suggests the presence of an orbital companion.
Again, the data tends to favor larger planets that exert a stronger gravitational influence, on shorter, closer orbits to their star.
Aside from these two prominent methods, it’s possible on occasion to directly image an exoplanet as it orbits its star. Though an extremely difficult thing to do, it may become more common in the JWST era.
According to astronomer Daniel Bayliss of the University of Warwick in the UK, this approach would uncover an almost opposite class of exoplanet to the short-orbit variety. In order to see an exoplanet without it being swamped by the glare of its parent star, the two bodies need to have a very wide separation. This means the direct imaging approach favors planets on relatively long orbits.
However, larger exoplanets would still be spotted more easily through this method, for obvious reasons.
“Each of the discovery methods has its own biases,” Bayliss explains.
Earth with its year-long loop around the Sun sits between the orbital extremes favored by different detection techniques, he adds, so “to find planets with a one year orbit is still very, very difficult.”
What’s out there?
By far, the most numerous group of exoplanets is a class that isn’t even represented in the Solar System. That’s the mini-Neptune – gas-enveloped exoplanets that are smaller than Neptune and larger than Earth in size.

Most of the confirmed exoplanets are on much shorter orbits than Earth; in fact, more than half have orbits of less than 20 days.
Most of the exoplanets we’ve found orbit solitary stars, much like our Sun. Fewer than 10 percent are in multi-star systems. Yet most of the stars in the Milky Way are members of a multi-star systems, with estimates as high as 80 percent seen in a partnership orbiting at least one other star.
Think about that for a moment, though. Does that mean that exoplanets are more common around single stars – or that exoplanets are harder to detect around multiple stars? The presence of more than one source of light can distort or obscure the very similar (but much smaller) signals we’re trying to detect from exoplanets, but it might also be reasoned that multi-star systems complicate planet formation in some way.
And this brings us back home again, back to our Solar System. As odd as home seems in the context of everything we’ve found, it might not be uncommon at all.
“I think it is fair enough to say that there’s actually some very common types of planets that are missing from our Solar System,” says Bayliss.
“Super Earths that look a little bit like Earth but have double the radius, we don’t have anything like that. We don’t have these mini-Neptunes. So I think it is fair enough to say that there are some very common planets that we don’t see in our own Solar System.
“Now, whether that makes our Solar System rare or not, I think I wouldn’t go that far. Because there could be a lot of other stars that have a Solar System-type set of planets that we just don’t see yet.”

On the brink of discovery
The first exoplanets were discovered just 30 years ago orbiting a pulsar, a star completely unlike our own. Since then, the technology has improved out of sight. Now that scientists know what to look for, they can devise better and better ways to find them around a greater diversity of stars.
And, as the technology advances, so too will our ability to find smaller and smaller worlds.
This means that exoplanet science could be on the brink of discovering thousands of worlds hidden from our current view. As Horner points out, in astronomy, there are way more small things than big things.
Red dwarf stars are a perfect example. They’re the most common type of star in the Milky Way – and they’re tiny, up to about half the mass of the Sun. They’re so small and dim that we can’t see them with the naked eye, yet they account for up to 75 percent of all stars in the galaxy.
Right now, when it comes to statistically understanding exoplanets, we’re operating with incomplete information, because there are types of worlds we just can’t see.
That is bound to change.
“I just have this nagging feeling that if you come back in 20 years time, you’ll look at those statements that mini-Neptunes are the most common kind of planets with about as much skepticism as you’d look back at statements from the early 1990s that said you’d only get rocky planets next to the star,” Horner tells ScienceAlert.
“Now, I could well be proved wrong. This is how science works. But my thinking is that when we get to the point that we can discover things that are Earth-sized and smaller, we’ll find that there are more things that are Earth-sized and smaller than there are things that are Neptune-sized.”
And maybe we’ll find that our oddball little planetary system, in all its quirks and wonders, isn’t so alone in the cosmos after all.
Will Neurotech Force Us to Update Human Rights?
One question for Nita Farahany, a philosopher at Duke University.
- By Brian Gallagher
- December 19, 2022
- Share


One question for Nita Farahany, a philosopher at Duke University who studies the implications of emerging neuroscience, genomics, and artificial intelligence for law and society.
Will neurotech force us to update human rights?
Yes. And that moment will pass us by quickly if we don’t seize on it, which would enable us to embrace and reap the benefits of the coming age of neural interface technology. That means recognizing the fundamental human right to cognitive liberty—our right to think freely, our self-determination over our brains and mental experiences. And then updating three existing rights: the right to privacy, freedom of thought, and self-determination.
Updating the right to privacy requires that we recognize explicitly a right to mental privacy. Freedom of thought is already recognized in international human rights law but has been focused on the right to free exercise of religion. We need to recognize a right against manipulation of thought, or having our thoughts used against us. And we’ve long recognized a collective right to self-determination of peoples or nations, but we need a right to self-determination over our own bodies, which will include, for example, a right to receiving information about ourselves.
If a corporation or an employer wants to implement fatigue monitoring in the workplace, for example, the default would be that the employee has a right to mental privacy. That means, if I’m tracking my brain data, a right to receive information about what is being tracked. It’s recognizing that by default people have rights over their cognitive liberty, and the exceptions have to be legally carved out. There would have to be robust consent, and robust information given to consumers about what the data is that is being collected, how it’s being used, and whether it can be used or commodified.
I’ve written a book that’s coming out in March, called The Battle for Your Brain: Defending the Right to Think Freely in the Age of Neurotechnology. One of the chapters in the book explores the line between persuasion and manipulation. I go into the example from Facebook experimenting on people, changing their timelines to feature negative or positive content. It was deeply offensive, and part of it was the lack of informed consent but a bigger part was it felt as if people’s emotions were being toyed with just to see if they could make somebody unhappy in ways that you could measure.
In a world of neurotechnology you can measure the effect of those experiments much more precisely because you can see what’s happening to the brain as you make those changes. But also, these technologies aren’t just devices that read the brain. Many of them are writing devices—you can make changes to the brain. That definitely requires that we think about who controls the technology and what they can do with it, including things to intentionally manipulate your brain that might cause you harm. What rules are we going to put into place to safeguard people against that?
I’m optimistic we can get this done. There’s already momentum at the human rights level. The value of the human rights level is that there will be lots of specific laws that will have to be implemented to realize a right to cognitive liberty locally, nationally, and across the world. But if you start with a powerful legal and moral obligation that’s universal, it’s easier to get those laws updated. People recognize the unique sensitivity of their thoughts and emotions. It’s not just the right to keep people out of your thoughts, or the right to not be manipulated. It’s a positive right to make choices about what your mental experiences are going to be like, whether that’s enhancements, or access to technology, or the ability to use and read out information from that technology. ![]()
Lead image: AndryDj / Shutterstock
- Brian GallagherPosted on December 19, 2022 Brian Gallagher is an associate editor at Nautilus. Follow him on Twitter @bsgallagher.
Get the Nautilus newsletter
The newest and most popular articles delivered right to your inbox!
January 4th 2023
INNOVATION
Could Getting Rid of Old Cells Help People Live Disease-Free for Longer?
Researchers are investigating medicines that selectively kill decrepit cells to promote healthy aging
Amber Dance, Knowable Magazine December 29, 2022
:focal(1035x729:1036x730)/https://tf-cmsv2-smithsonianmag-media.s3.amazonaws.com/filer_public/9a/93/9a93ecd0-867e-4514-a75c-94d5d555b18f/gettyimages-1396817149.jpg)
James Kirkland started his career in 1982 as a geriatrician, treating aging patients. But he found himself dissatisfied with what he could offer them.
“I got tired of prescribing wheelchairs, walkers and incontinence devices,” recalls Kirkland, now at the Mayo Clinic in Rochester, Minnesota. He knew that aging is considered the biggest risk factor for chronic illness, but he was frustrated by his inability to do anything about it. So Kirkland went back to school to learn the skills he’d need to tackle aging head-on, earning a PhD in biochemistry at the University of Toronto. Today, he and his colleague Tamar Tchkonia, a molecular biologist at the Mayo Clinic, are leaders in a growing movement to halt chronic disease by protecting brains and bodies from the biological fallout of aging.
If these researchers are successful, they’ll have no shortage of customers: People are living longer, and the number of Americans age 65 and older is expected to double, to 80 million, between 2000 and 2040. While researchers like Kirkland don’t expect to extend lifespan, they hope to lengthen “health span,” the time that a person lives free of disease.
One of their targets is decrepit cells that build up in tissues as people age. These “senescent” cells have reached a point—due to damage, stress or just time—when they stop dividing, but don’t die. While senescent cells typically make up only a small fraction of the overall cell population, they accounted for up to 36 percent of cells in some organs in aging mice, one study showed. And they don’t just sit there quietly. Senescent cells can release a slew of compounds that create a toxic, inflamed environment that primes tissues for chronic illness. Senescent cells have been linked to diabetes, stroke, osteoporosis and several other conditions of aging.
These noxious cells, along with the idea that getting rid of them could mitigate chronic illnesses and the discomforts of aging, are getting serious attention. The U.S. National Institutes of Health is investing $125 million in a new research effort, called SenNet, that aims to identify and map senescent cells in the human body as well as in mice over the natural lifespan. And the National Institute on Aging has put up more than $3 million over four years for the Translational Geroscience Network (TGN) multicenter team led by Kirkland that is running preliminary clinical trials of potential antiaging treatments. Drugs that kill senescent cells—called senolytics—are among the top candidates. Small-scale trials of these are already underway in people with conditions including Alzheimer’s, osteoarthritis and kidney disease.
“It’s an emerging and incredibly exciting—and maybe even game-changing—area,” says John Varga, chief of rheumatology at the University of Michigan Medical School in Ann Arbor, who isn’t part of the TGN.
But he and others sound a note of caution as well, and some scientists think the field’s potential has been overblown. “There’s a lot of hype,” says Varga. “I do have, I would say, a very healthy skepticism.” He warns his patients of the many unknowns and tells them that trying senolytic supplementation on their own could be dangerous.
Researchers are still untangling the biology of senescent cells, not only in aging animals but also in younger ones—even in embryos, where the aging out of certain cells is crucial for proper development. So far, evidence that destroying senescent cells helps to improve health span mostly comes from laboratory mice. Only a couple of preliminary human trials have been completed, with hints of promise but far from blockbuster results.
Even so, Kirkland and Tchkonia speculate that senolytics might eventually help not only with aging but also with conditions suffered by younger people due to injury or medical treatments such as chemotherapy. “There may be applications all over the place,” muses Kirkland.
/https://tf-cmsv2-smithsonianmag-media.s3.amazonaws.com/filer_public/e2/46/e2465bf3-821e-4ddc-9051-b832a1efbf29/p-normal-and-senescent-cells.jpg)
Good cells gone bad
Biologists first noticed senescence when they began growing cells in lab dishes more than 60 years ago. After about 50 cycles of cells first growing, then dividing, the rate of cell division slows and ultimately ceases. When cells reach this state of senescence, they grow larger and start exhibiting a variety of genetic abnormalities. They also accumulate extra lysosomes, baglike organelles that destroy cellular waste. Scientists have found a handy way to identify many senescent cells by using stains that turn blue in the presence of a lysosome enzyme, called beta-galactosidase, that’s often overactive in these cells.
Scientists have also discovered hundreds of genes that senescent cells activate to shut down the cells’ replication cycle, change their biology and block natural self-destruct mechanisms. Some of these genes produce a suite of immune molecules, growth factors and other compounds. The fact that specific genes consistently turn on in senescent cells indicates there may be more to senescence than just cells running out of steam. It suggests that senescence is a cellular program that evolved for some purpose in healthy bodies. Hints at that purpose have emerged from studies of creatures far earlier in their lifespan—even before birth.
Cell biologist Bill Keyes was working on senescence in embryos back in the early 2000s. When he stained healthy mouse and chick embryos to look for beta-galactosidase, little blue spots lit up in certain tissues. He soon met up with Manuel Serrano, a cell biologist at the Institute for Research in Biomedicine in Barcelona, who’d noticed the same thing. Cells with signs of senescence turned up in the developing brain, ear and limbs, Keyes and Serrano reported in 2013.
Keyes, now at the Institute of Genetics and Molecular and Cellular Biology in Strasbourg, France, focused on mouse and chick embryonic limbs, where a thread of temporary tissue forms across the future toe-tips. Unlike most embryonic cells, the cells in this thread of tissue disappear before the animal is born. They release chemicals that help the limb develop, and once their work is done, they die. At a molecular level, they look a lot like senescent cells.
Serrano, meanwhile, looked at cells in an organ that exists only in embryos: a temporary kidney, called the mesonephros, that forms near the heart. Once the final kidneys develop, the mesonephros disappears. Here, too, beta-galactosidase and other compounds linked to senescence appeared in mouse embryos.
The cells in these temporary tissues probably disappear because they are senescent. Certain compounds made by senescent cells call out to the immune system to come in and destroy the cells once their work is done. Scientists think the short-term but crucial jobs these cells perform could be the reason senescence evolved in the first place.
Other studies suggest that senescent cells may also promote health in adult animals. Judith Campisi, a cell biologist at the Buck Institute for Research on Aging in Novato, California, and others have found senescent cells in adult mice, where they participate in wound healing. Connective-tissue cells called fibroblasts fill in a wound, but if they stick around, they form abnormal scar tissue. During normal wound healing, they turn senescent, releasing compounds that both promote repair of the tissue and call immune cells to come in and destroy them.
In other words, the emergence of senescent cells in aging people isn’t necessarily a problem in and of itself. The problem seems to be that they hang around for too long. Serrano suspects this happens because the immune system in aging individuals isn’t up to the task of eliminating them all. And when senescent cells stay put, the cocktail of molecules they produce and the ongoing immune response can damage surrounding tissues.
Senescence can also contribute to cancer, as Campisi has described in the Annual Review of Physiology, but the relationship is multifaceted. Senescence itself is a great defense against cancer—cells that don’t divide don’t form tumors. On the other hand, the molecules senescent cells emit can create an inflamed, cancer-promoting environment. So if a senescent cell arises near a cell that’s on its way to becoming cancerous, it might alter the locale enough to push that neighbor cell over the edge. In fact, Campisi reported in 2001 that injecting mice with senescent cells made tumors grow bigger faster.
Mighty mice
If senescent cells in an aging body are bad, removing them should be good. To test this idea, Darren Baker, a molecular cell biologist at the Mayo Clinic, devised a way to kill senescent cells in mice. Baker genetically engineered mice so that when their cells turned senescent, those cells became susceptible to a certain drug. The researchers began injecting the drug twice a week once the mice turned 1 year old—that’s about middle age for a lab mouse.
Treated mice maintained healthier kidney, heart, muscle and fat tissue compared with untreated mice, and though they were still susceptible to cancer, tumors appeared later in life, the researchers reported in studies in 2011 and 2016. The rodents also lived, on average, five or six months longer.
These results generated plenty of interest, Baker recalls, and set senescence biology on the path toward clinical research. “That was the boom—a new era for cellular senescence,” says Viviana Perez, former program officer for the SenNet consortium at the National Institute on Aging.
Baker followed up with a study of mice that had been genetically modified to develop characteristics of Alzheimer’s. Getting rid of senescent cells staved off the buildup of toxic proteins in the brain, he reported, and seemed to help the mice to retain mental acuity, as measured by their ability to remember a new smell.
Of course, geriatricians can’t go about genetically engineering retirees, so Kirkland, Tchkonia and colleagues went hunting for senolytic drugs that would kill senescent cells while leaving their healthy neighbors untouched. They reasoned that since senescent cells appear to be resistant to a process called apoptosis, or programmed cell death, medicines that unblock that process might have senolytic properties.
/https://tf-cmsv2-smithsonianmag-media.s3.amazonaws.com/filer_public/6c/75/6c75e503-a297-4dbc-8ce4-1eb04a4f6bb4/g-senescent-cells-and-effects-alt.png)
Some cancer drugs do this, and the researchers included several of these in a screen of 46 compounds they tested on senescent cells grown in lab dishes. The study turned up two major winners: One was the cancer drug dasatinib, an inhibitor of several natural enzymes that appears to make it possible for the senescent cells to self-destruct. The other was quercetin, a natural antioxidant that’s responsible for the bitter flavor of apple peels and that also inhibits several cellular enzymes. Each drug worked best on senescent cells from different tissues, the scientists found, so they decided to use them both, in a combo called D+Q, in studies with mice.
In one study, Tchkonia and Kirkland gave D+Q to 20-month-old mice and found that the combination improved the rodents’ walking speed and endurance in lab tests, as well as their grip strength. And treating 2-year-old mice—the equivalent of a 75- to 90-year-old human—with D+Q every other week extended their remaining lifespan by about 36 percent, compared with mice that didn’t receive senolytics, the researchers reported in 2018. Tchkonia, Kirkland and Baker all hold patents related to treating diseases by eliminating senescent cells.
To the clinic
Scientists have since discovered several other medications with senolytic effects, though D+Q remains a favorite pairing. Further studies from several research groups reported that senolytics appear to protect mice against a variety of conditions of aging, including the metabolic dysfunction associated with obesity, vascular problems associated with atherosclerosis and bone loss akin to osteoporosis.
“That’s a big deal, collectively,” says Laura Niedernhofer, a biochemist at the University of Minnesota Medical School in Minneapolis who is a collaborator on some of these studies and a member of the TGN clinical trials collaboration. “It would be a shame not to test them in humans.”
A few small human trials have been completed. The first, published in 2019, addressed idiopathic pulmonary fibrosis, a fatal condition in which the lungs fill up with thick scar tissue that interferes with breathing. It’s most common in people 60 or older, and there’s no cure. In a small pilot study, Kirkland, Tchkonia and collaborators administered D+Q to 14 people with the condition, three times a week for three weeks. They reported notable improvement in the ability of participants to stand up from a chair and to walk for six minutes. But the study had significant caveats: In addition to its small size and short duration, there was no control group, and every participant knew they’d received D+Q. Moreover, the patients’ lung function didn’t improve, nor did their frailty or overall health.
Niedernhofer, who wasn’t involved in the trial, calls the results a “soft landing”: There seemed to be something there, but no major benefits emerged. She says she would have been more impressed with the results if the treatment had reduced the scarring in the lungs.
The TGN is now running several small trials for conditions related to aging, and other diseases, too. Kirkland thinks that senescence may even be behind conditions that affect young people, such as osteoarthritis due to knee injuries and frailty in childhood cancer survivors.
/https://tf-cmsv2-smithsonianmag-media.s3.amazonaws.com/filer_public/ee/fb/eefbd3e0-84bc-46ad-bd34-c52f6dd839b4/g-senolytics-clinical-trials-alt.png)
Tchkonia and Kirkland are also investigating how space radiation affects indications of senescence in the blood and urine of astronauts, in conjunction with two companies, SpaceX and Axiom Space. They hypothesize that participants in future long-term missions to Mars might have to monitor their bodies for senescence or pack senolytics to stave off accelerated cellular aging caused by extended exposure to radiation.
Kirkland is also collaborating with researchers who are investigating the use of senolytics to expand the pool of available transplant organs. Despite desperate need, about 24,000 organs from older donors are left out of the system every year because the rate of rejection is higher for these than for younger organs, says Stefan Tullius, chief of transplant surgery at Brigham and Women’s Hospital in Boston. In heart transplant experiments with mice, he reported that pretreating older donor mice with D+Q before transplant into younger recipients resulted in the donor organs working “as well or slightly better” than hearts from young donors.
“That was huge,” says Tullius. He hopes to be doing clinical trials in people within three years.
Healthy skepticism
Numerous medical companies have jumped on the anti-senescence bandwagon, notes Paul Robbins, a molecular biologist at the University of Minnesota Medical School. But results have been mixed. One front-runner, Unity Biotechnology of South San Francisco, California, dropped a top program in 2020 after its senolytic medication failed to reduce pain in patients with knee osteoarthritis.
“I think we just don’t know enough about the right drug, the right delivery, the right patient, the right biomarker,” says the University of Michigan’s Varga, who is not involved with Unity. More recently, however, the company reported progress in slowing diabetic macular edema, a form of swelling in the back of the eye due to high blood sugar.
Despite the excitement, senolytic research remains in preliminary stages. Even if the data from TGN’s initial, small trials looks good, they won’t be conclusive, says network member Robbins—who nonetheless thinks positive results would be a “big deal.” Success in a small study would suggest it’s worth investing in larger studies, and in the development of drugs that are more potent or specific for senescent cells.
“I’m urging extreme caution,” says Campisi—who is herself a cofounder of Unity and holds several patents related to anti-senescence treatments. She’s optimistic about the potential for research on aging to improve health, but she worries that moving senolytics quickly into human trials, as some groups are doing, could set the whole field back. That’s what happened with gene therapy in the late 1990s when an experimental treatment killed a study volunteer. “I hope they don’t kill anyone, seriously,” she says.
Side effects are an ongoing concern. For example, dasatinib (the D in D+Q) has a host of side effects ranging from nosebleeds to fainting to paralysis.
But Kirkland thinks that may not be an insurmountable problem. He notes that these side effects show up only in cancer patients taking the drug regularly for months at a time, whereas anti-senescence treatments might not need to be taken so often—once every two or three months might be enough to keep the population of senescent cells under control.
Another way to reduce the risks would be to make drugs that target senescent cells in specific tissues, Niedernhofer and Robbins note in the Annual Review of Pharmacology and Toxicology. For example, if a person has senescent cells in their heart, they could take a medicine that targets only those cells, leaving any other senescent cells in the body—which still might be doing some good—alone.
For that strategy to work, though, doctors would need better ways to map senescent cells in living people. While identifying such biomarkers is a major goal for SenNet, Campisi suspects it will be hard to find good ones. “It’s not a simple problem,” she says.
A lot of basic and clinical research must happen first, but if everything goes right, senolytics might someday be part of a personalized medicine plan: The right drugs, at the right time, could help keep aging bodies healthy and nimble. It may be a long shot, but to many researchers, the possibility of nixing walkers and wheelchairs for many patients makes it one worth taking.
Knowable Magazine is an independent journalistic endeavor from Annual Reviews.
AgingBiologyBrainCancerChemistryDisease and IllnessesGeneticsHealthMedicineNeurosciencev
January 1st 2023
The Year in Computer Science
Computer scientists this year learned how to transmit perfect secrets, why transformers seem so good at everything, and how to improve on decades-old algorithms (with a little help from AI).


December 21, 2022
2022 in Reviewalgorithmsartificial intelligencebrainscomputational complexitycomputer sciencecryptographyentanglementinformation theorymachine learningmathematicsneural networksphysicsquantum computingquantum cryptographyquantum physicsYear in ReviewAll topics

Introduction
As computer scientists tackle a greater range of problems, their work has grown increasingly interdisciplinary. This year, many of the most significant computer science results also involved other scientists and mathematicians. Perhaps the most practical involved the cryptographic questions underlying the security of the internet, which tend to be complicated mathematical problems. One such problem — the product of two elliptic curves and their relation to an abelian surface — ended up bringing down a promising new cryptography scheme that was thought to be strong enough to withstand an attack from a quantum computer. And a different set of mathematical relationships, in the form of one-way functions, will tell cryptographers if truly secure codes are even possible.
Computer science, and quantum computing in particular, also heavily overlaps with physics. In one of the biggest developments in theoretical computer science this year, researchers posted a proof of the NLTS conjecture, which (among other things) states that a ghostly connection between particles known as quantum entanglement is not as delicate as physicists once imagined. This has implications not just for our understanding of the physical world, but also for the myriad cryptographic possibilities that entanglement makes possible.
And artificial intelligence has always flirted with biology — indeed, the field takes inspiration from the human brain as perhaps the ultimate computer. While understanding how the brain works and creating brainlike AI has long seemed like a pipe dream to computer scientists and neuroscientists, a new type of neural network known as a transformer seems to process information similarly to brains. As we learn more about how they both work, each tells us something about the other. Perhaps that’s why transformers excel at problems as varied as language processing and image classification. AI has even become better at helping us make better AI, with new “hypernetworks” helping researchers train neural networks faster and at a lower cost. So now the field is not only helping other scientists with their work, but also helping its own researchers achieve their goals.
Share this article
Newsletter
Get Quanta Magazine delivered to your inbox

Introduction
Entangled Answers
When it came to quantum entanglement, a property that intimately connects even distant particles, physicists and computer scientists were at an impasse. Everyone agreed that a fully entangled system would be impossible to describe fully. But physicists thought it might be easier to describe systems that were merely close to being fully entangled. Computer scientists disagreed, saying that those would be just as impossible to calculate — a belief formalized into the “no low-energy trivial state” (NLTS) conjecture. In June a team of computer scientists posted a proof of it. Physicists were surprised, since it implied that entanglement is not necessarily as fragile as they thought, and computer scientists were happy to be one step closer to proving a seminal question known as the quantum probabilistically checkable proof theorem, which requires NLTS to be true.
This news came on the heels of results from late last year showing that it’s possible to use quantum entanglement to achieve perfect secrecy in encrypted communications. And this October researchers successfully entangled three particles over considerable distances, strengthening the possibilities for quantum encryption.

Introduction
Transforming How AI Understands
For the past five years, transformers have been revolutionizing how AI processes information. Developed originally to understand and generate language, the transformer processes every element in its input data simultaneously, giving it a big-picture understanding that lends it improved speed and accuracy compared to other language networks, which take a piecemeal approach. This also makes it unusually versatile, and other AI researchers are putting it to work in their fields. They have discovered that the same principles can also enable them to upgrade tools for image classification and for processing multiple kinds of data at once. However, these benefits come at the cost of more training than non-transformer models need. Researchers studying how transformers work learned in March that part of their power comes from their ability to attach greater meaning to words, rather than simply memorize patterns. Transformers are so adaptable, in fact, that neuroscientists have begun modeling human brain functions with transformer-based networks, suggesting a fundamental similarity between artificial and human intelligence.

Introduction
Breaking Down Cryptography
The safety of online communications is based on the difficulty of various math problems — the harder a problem is to solve, the harder a hacker must work to break it. And because today’s cryptography protocols would be easy work for a quantum computer, researchers have sought new problems to withstand them. But in July, one of the most promising leads fell after just an hour of computation on a laptop. “It’s a bit of a bummer,” said Christopher Peikert, a cryptographer at the University of Michigan.
The failure highlights the difficulty of finding suitable questions. Researchers have shown that it’s only possible to create a provably secure code — one which could never fall — if you can prove the existence of “one-way functions,” problems that are easy to do but hard to reverse. We still don’t know if they exist (a finding that would help tell us what kind of cryptographic universe we live in), but a pair of researchers discovered that the question is equivalent to another problem called Kolmogorov complexity, which involves analyzing strings of numbers: One-way functions and real cryptography are possible only if a certain version of Kolmogorov complexity is hard to compute.

Introduction
Machines Help Train Machines
In recent years, the pattern recognition skills of artificial neural networks have supercharged the field of AI. But before a network can get to work, researchers must first train it, fine-tuning potentially billions of parameters in a process that can last for months and requires huge amounts of data. Or they could get a machine to do it for them. With a new kind of “hypernetwork” — a network that processes and spits out other networks — they may soon be able to. Named GHN-2, the hypernetwork analyzes any given network and provides a set of parameter values that were shown in a study to be generally at least as effective as those in networks trained the traditional way. Even when it didn’t provide the best possible parameters, GHN-2’s suggestions still offered a starting point that was closer to the ideal, cutting down the time and data required for full training.
This summer, Quanta also examined another new approach to helping machines learn. Known as embodied AI, it allows algorithms to learn from responsive three-dimensional environments, rather than static images or abstract data. Whether they’re agents exploring simulated worlds or robots in the real one, these systems learn fundamentally differently — and, in many cases, better — than ones trained using traditional approaches.
Mahmet Emin Güzel for Quanta Magazine
Introduction
Improved Algorithms
This year, with the rise of more sophisticated neural networks, computers made further strides as a research tool. One such tool seemed particularly well suited to the problem of multiplying two-dimensional tables of numbers called matrices. There’s a standard way to do it, but it becomes cumbersome as matrices grow larger, so researchers are always looking for a faster algorithm that uses fewer steps. In October, researchers at DeepMind announced that their neural network had discovered faster algorithms for multiplying certain matrices. But experts cautioned that the breakthrough represented the arrival of a new tool for solving a problem, not an entirely new era of AI solving these problems on its own. As if on cue, a pair of researchers built on the new algorithms, using traditional tools and methods to improve them.
Researchers in March also published a faster algorithm to solve the problem of maximum flow, one of the oldest questions in computer science. By combining past approaches in novel ways, the team created an algorithm that can determine the maximum possible flow of material through a given network “absurdly fast,” according to Daniel Spielman of Yale University. “I was actually inclined to believe … algorithms this good for this problem would not exist.”

Introduction
New Avenues for Sharing Information
Mark Braverman, a theoretical computer scientist at Princeton University, has spent more than a quarter of his life working on a new theory of interactive communication. His work allows researchers to quantify terms like “information” and “knowledge,” not just allowing for a greater theoretical understanding of interactions, but also creating new techniques that enable more efficient and accurate communication. For this achievement and others, the International Mathematical Union this July awarded Braverman the IMU Abacus Medal, one of the highest honors in theoretical computer science.
The Quanta Newsletter
December 25th 2022
The paradox of light goes beyond wave-particle duality
Light carries with it the secrets of reality in ways we cannot completely understand.

Key Takeaways
- Light is the most mysterious of all things we know exist.
- Light is not matter; it is both wave and particle — and it’s the fastest thing in the Universe.
- We are only beginning to understand light’s secrets.
Share The paradox of light goes beyond wave-particle duality on Facebook
Share The paradox of light goes beyond wave-particle duality on Twitter
Share The paradox of light goes beyond wave-particle duality on LinkedIn
This is the third in a series of articles exploring the birth of quantum physics.
Light is a paradox. It is associated with wisdom and knowledge, with the divine. The Enlightenment proposed the light of reason as the guiding path toward truth. We evolved to identify visual patterns with great accuracy — to distinguish the foliage from the tiger, or shadows from an enemy warrior. Many cultures identify the sun as a god-like entity, provider of light and warmth. Without sunlight, after all, we would not be here.
Yet the nature of light is a mystery. Sure, we have learned a tremendous amount about light and its properties. Quantum physics has been essential along this path, changing the way we describe light. But light is weird. We cannot touch it the way we touch air or water. It is a thing that is not a thing, or at least it is not made of the stuff we associate with things.
If we traveled back to the 17th century, we could follow Isaac Newton’s disagreements with Christiaan Huygens on the nature of light. Newton would claim that light is made of tiny, indivisible atoms, while Huygens would counter that light is a wave that propagates on a medium that pervades all of space: the ether. They were both right, and they were both wrong. If light is made of particles, what particles are these? And if it is a wave propagating across space, what’s this weird ether?
Light magic
We now know that we can think of light in both ways — as a particle, and as a wave. But during the 19th century the particle theory of light was mostly forgotten, because the wave theory was so successful, and something could not be two things. In the early 1800s Thomas Young, who also helped decipher the Rosetta Stone, performed beautiful experiments showing how light diffracted as it passed through small slits, just like water waves were known to do. Light would move through the slit and the waves would interfere with one another, creating bright and dark fringes. Atoms couldn’t do that.
But then, what was the ether? All great physicists of the 19th century, including James Clerk Maxwell, who developed the beautiful theory of electromagnetism, believed the ether was there, even if it eluded us. After all, no decent wave could propagate in empty space. But this ether was quite bizarre. It was perfectly transparent, so we could see faraway stars. It had no mass, so it wouldn’t create friction and interfere with planetary orbits. Yet it was very rigid, to allow for the propagation of the ultra-fast light waves. Pretty magical, right? Maxwell had shown that if an electric charge oscillated up and down, it would generate an electromagnetic wave. This was the electric and magnetic fields tied up together, one bootstrapping the other as they traveled through space. And more amazingly, this electromagnetic wave would propagate at the speed of light, 186,282 miles per second. You blink your eyes and light goes seven and a half times around the Earth.
Maxwell concluded that light is an electromagnetic wave. The distance between two consecutive crests is a wavelength. Red light has a longer wavelength than violet light. But the speed of any color in empty space is always the same. Why is it about 186,000 miles per second? No one knows. The speed of light is one of the constants of nature, numbers we measure that describe how things behave.
Steady as a wave, hard as a bullet
A crisis started in 1887 when Albert Michelson and Edward Morley performed an experiment to demonstrate the existence of the ether. They couldn’t prove a thing. Their experiment failed to show that light propagated in an ether. It was chaos. Theoretical physicists came up with weird ideas, saying the experiment failed because the apparatus shrunk in the direction of the motion. Anything was better than accepting that light actually can travel in empty space.
And then came Albert Einstein. In 1905, the 26-year-old patent officer wrote two papers that completely changed the way we picture light and all of reality. (Not too shabby.) Let’s start with the second paper, on the special theory of relativity.
Subscribe for counterintuitive, surprising, and impactful stories delivered to your inbox every Thursday
Fields marked with an * are required
Einstein showed that if one takes the speed of light to be the fastest speed in nature, and assumes that this speed is always the same even if the light source is moving, then two observers moving with respect to each other at a constant speed and making an observation need to correct for their distance and time measurements when comparing their results. So, if one is in a moving train while the other is standing at a station, the time intervals of the measurements they make of the same phenomenon will be different. Einstein provided a way for the two to compare their results in a way that allows these to agree with each other. The corrections showed that light could and should propagate in empty space. It had no need for an ether.
Einstein’s other paper explained the so-called photoelectric effect, which was measured in the lab in the 19th century but remained a total mystery. What happens if light is shined onto a metal plate? It depends on the light. Not on how bright it is, but on its color — or more appropriately stated, its wavelength. Yellow or red light does nothing. But shine a blue or violet light on the plate, and the plate actually acquires an electrical charge. (Hence the term photoelectric.) How could light electrify a piece of metal? Maxwell’s wave theory of light, so good at so many things, could not explain this.
The young Einstein, bold and visionary, put forth an outrageous idea. Light can be a wave, sure. But it can also be made of particles. Depending on the circumstance, or on the type of experiment, one or the other description prevails. For the photoelectric effect, we could picture little “bullets” of light hitting the electrons on the metal plate and kicking them out like billiard balls flying off a table. Having lost electrons, the metal now holds a surplus positive charge. It’s that simple. Einstein even provided a formula for the energy of the flying electrons and equated it to the energy of the incoming light bullets, or photons. The energy for the photons is E = hc/L, where c is the speed of light, L its wavelength, and h is Planck’s constant. The formula tells us that smaller wavelengths mean more energy — more kick for the photons.
Einstein won the Nobel prize for this idea. He essentially suggested what we now call the wave-particle duality of light, showing that light can be both particle and wave and will manifest differently depending on the circumstance. The photons — our light bullets — are the quanta of light, the smallest light packets possible. Einstein thus brought quantum physics into the theory of light, showing that both behaviors are possible.
I imagine Newton and Huygens are both smiling in heaven. These are the photons that Bohr used in his model of the atom, which we discussed last week. Light is both particle and wave, and it is the fastest thing in the cosmos. It carries with it the secrets of reality in ways we cannot completely understand. But understanding its duality was an important step for our perplexed minds.
Why black holes spin at nearly the speed of light
Black holes aren’t just the densest masses in the Universe, but they also spin the fastest of all massive objects. Here’s why it must be so.

Key Takeaways
- Black holes are some of the most enigmatic, extreme objects in the entire Universe, with more mass compressed into a tiny volume than any other object.
- But black holes aren’t just extremely massive, they’re also incredibly fast rotators. Many black holes, from their measured spins, are spinning at more than 90% the speed of light.
- This might seem like a puzzle, but physics not only has an explanation for why, but shows us that it’s very difficult to create black holes that spin slowly relative to the speed of light. Here’s why.
Share Why black holes spin at nearly the speed of light on Facebook
Share Why black holes spin at nearly the speed of light on Twitter
Share Why black holes spin at nearly the speed of light on LinkedIn
Whenever you take a look out there at the vast abyss of the deep Universe, it’s the points of light that stand out the most: stars and galaxies. While the majority of the light that you’ll first notice does indeed come from stars, a deeper look, going far beyond the visible portion of the electromagnetic spectrum, shows that there’s much more out there. The brightest, most massive stars, by their very nature, have the shortest lifespans, as they burn through their fuel far more quickly than their lower-mass counterparts. Once they’ve reached their limits and can fuse elements no further, they reach the end of their lives and become stellar corpses.
These corpses come in multiple varieties: white dwarfs for the lowest-mass (e.g., Sun-like) stars, neutron stars for the next tier up, and black holes for the most massive stars of all. These compact objects give off electromagnetic emissions spanning wavelengths from radio to X-ray light, revealing properties that range from mundane to absolutely shocking. While most stars themselves may spin relatively slowly, black holes rotate at nearly the speed of light. This might seem counterintuitive, but under the laws of physics, it couldn’t be any other way. Here’s why.

The closest analogue we have to one of those extreme objects in our own Solar System is the Sun. In another 7 billion years or so, after becoming a red giant and burning through the helium fuel that’s built up within its core, it will end its life by blowing off its outer layers while its core contracts down to a stellar remnant: the most gentle of all major types of stellar death.
The outer layers will create a sight known as a planetary nebula, which comes from the blown-off gases getting ionized and illuminated from the contracting central core. This nebula will glow for tens of thousands of years before cooling off and becoming neutral again, generally returning that material to the interstellar medium. When the opportunity then arises, those processed atoms will participate in future generations of star formation.
But the inner core, largely composed of carbon and oxygen, will contract down as far as it possibly can. In the end, gravitational collapse will only be stopped by the particles — atoms, ions, and electrons — that the remnant of our Sun will be made of.

So long as you remain below a critical mass threshold, the Chandrasekhar mass limit, the quantum properties inherent to those particles will be sufficient to hold the stellar remnant up against gravitational collapse. The endgame for a Sun-like star’s core will be a degenerate state known as a white dwarf. It will possess a sizable fraction of the mass of its parent star, but crammed into a tiny fraction of the volume: approximately the size of Earth.
Astronomers now know enough about stars and stellar evolution to describe what happens during this process. For a star like our Sun, approximately 60% of its mass will get expelled in the outer layers, while the remaining 40% remains in the core. The more massive a star becomes, the more mass, percentage-wise, gets blown off in its outer layers, with less being retained in the core. For the most massive stars that suffer the same fate as our Sun, possessing about 7-8 times the Sun’s mass, the mass fraction remaining in the core comes all the way down to about 18% of the original star’s mass.
This has happened nearby relatively recently, as the brightest star in Earth’s sky, Sirius, has a white dwarf companion, visible in the Hubble image below.

Sirius A is a little bit brighter and more massive than our Sun, and we believe that its binary companion, Sirius B, was once even more massive than Sirius A. Because the more massive stars burn through their nuclear fuel more quickly than lower-mass ones, Sirius B likely ran out of fuel some time ago. Today, Sirius A remains burning through its hydrogen fuel, and dominates that system in terms of mass and brightness. While Sirius A, today, weighs in at about twice the mass of our Sun, Sirius B is only approximately equal to our Sun’s mass.
However, based on observations of the white dwarfs that happen to pulse, we’ve learned a valuable lesson. Rather than taking multiple days or even (like our Sun) approximately a month to complete a full rotation, like normal stars tend to do, white dwarfs complete a full 360° rotation in as little as an hour. This might seem bizarre, but if you’ve ever seen a figure skating routine, the same principle that explains a spinning skater who pulls their arms in explains the white dwarfs rotational speed: the law of conservation of angular momentum.

Angular momentum is simply a measure of “How much rotational and/or orbital motion does a mass have to it?” If you puff that massive object up so that its mass is farther from its rotational center, it has to slow down in its rotational speed in order to conserve angular momentum. Similarly, if you compress a massive object down, so that more of its mass is closer to the center of its axis-of-rotation, it will have to speed up in its rotational speed, making more revolutions-per-second, to keep angular momentum conserved.
What happens, then, if you were to take a star like our Sun — with the mass, volume, and rotation speed of the Sun — and compressed it down into a volume the size of the Earth: a typical size for a white dwarf?
Believe it or not, if you make the assumption that angular momentum is conserved, and that both the Sun and the compressed version of the Sun we’re imagining are spheres, this is a completely solvable problem with only one possible answer. If we go conservative, and assume the entirety of the Sun rotates once every 33 days (the longest amount of time it takes any part of the Sun’s photosphere to complete one 360° rotation) and that only the inner 40% of the Sun becomes a white dwarf, you get a remarkable answer: the Sun, as a white dwarf, will complete a rotation in just 25 minutes.

By bringing all of that mass close in to the stellar remnant’s axis of rotation, we ensure that its rotational speed must rise. In general, if you halve the radius that an object has as it rotates, its rotational speed increases by a factor of four; rotational speed is inversely proportional to the square of a rotating mass’s radius. If you consider that it takes approximately 109 Earths to go across the diameter of the Sun, you can derive the same answer for yourself. (In reality, white dwarfs generally rotate a little more slowly, as the outermost layers get blown off, and only the interior “core” material contracts down to form a white dwarf.)
Unsurprisingly, then, you might start to ask about neutron stars or black holes: even more extreme objects. A neutron star is typically the product of a much more massive star ending its life in a supernova, where the particles in the core get so compressed that it behaves as one giant atomic nucleus composed almost exclusively (90% or more) of neutrons. Neutron stars are typically twice the mass of our Sun, but just about 10-to-40 km across. They rotate far more rapidly than any known star or white dwarf ever could.

Even the most naïve estimate you could make for the rotational speed of a neutron star — again, in analogy with our Sun — illustrates just how rapidly we can expect a neutron star to spin. If you repeated the thought experiment of compressing the entire Sun down into a smaller volume, but this time used one that was merely 40 kilometers in diameter, you’d get a much, much more rapid rotation rate than you ever could for a white dwarf: about 10 milliseconds. That same principle that we previously applied to a figure skater, about the conservation of angular momentum, leads us to the conclusion that neutron stars could complete more than 100 full rotations in a single second.
Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!
Fields marked with an * are required
In fact, this lines up perfectly with our actual observations. Some neutron stars emit radio pulses along Earth’s line-of-sight to them: pulsars. We can measure the pulse periods of these objects, and while some of them take approximately a full second to complete a rotation, some of them rotate in as little as 1.3 milliseconds, up to a maximum of 766 rotations-per-second.

The fastest-spinning neutron stars known are called millisecond pulsars, and they really do rotate at incredibly fast speeds. At their surfaces, those rotation rates are indeed relativistic: meaning they reach speeds that are a significant fraction of the speed of light. The most extreme examples of such neutron stars can reach speeds exceeding 50% the speed of light at the outer surface of these neutron stars.
But that doesn’t even approach the true astrophysical limits found in the Universe. Neutron stars aren’t the densest objects in the Universe; that honor goes to black holes, which take all the mass you’d find in a neutron star — more, in fact — and compress it down into a region of space where even an object moving at the speed of light couldn’t escape from it.
If you compressed the Sun down into a volume just 3 kilometers in radius, that would force it to become a black hole. And yet, the conservation of angular momentum would mean that much of that internal region would experience frame-dragging so severe that space itself would get dragged at speeds approaching the speed of light, even outside of the Schwarzschild radius of the black hole. The more you compress that mass down, the faster the fabric of space itself gets dragged.

Realistically, we can’t measure the frame-dragging of space itself in the vicinity of a black hole. But we can measure the frame-dragging effects on the matter that happens to be present within that space. For black holes, that means looking at the accretion disks and accretion flows found around these black holes that exist in matter-rich environments. Perhaps paradoxically, the smallest mass black holes, which have the smallest event horizons, actually have the largest amounts of spatial curvature at and near their event horizons.
You might think, therefore, that they’d make the best laboratories for testing these frame dragging effects. But nature surprised us on that front: a supermassive black hole at the center of galaxy NGC 1365 — which also happens to be one of the first galaxies imaged by the James Webb Space Telescope — has had the radiation emitted from the volume outside of it detected and measured, revealing its speed. Even at these large distances, the material spins at 84% the speed of light. If you insist that angular momentum be conserved, it couldn’t have turned out any other way.

Subsequently, we’ve inferred the spins of black holes that have merged together with gravitational wave observatories such as LIGO and Virgo, and found that some black holes spin at the theoretical maximum: around ~95% the speed of light. It’s a tremendously difficult thing to intuit: the notion that black holes should spin at almost the speed of light. After all, the stars that black holes are built from rotate extremely slowly, even by Earth’s standards of one rotation every 24 hours. Yet if you remember that most of the stars in our Universe also have enormous volumes, you’ll realize that they contain an enormous amount of angular momentum.
If you compress that volume down to be very small, those objects have no choice. If angular momentum has to be conserved, all they can do is spin up their rotational speeds until they almost reach the speed of light. At that point, gravitational waves will kick in, and some of that energy (and angular momentum) gets radiated away, bringing it back down to below the theoretical maximum value. If not for those processes, black holes might not be black after all, instead revealing naked singularities at their centers. In this Universe, black holes have no choice but to rotate at extraordinary speeds. Perhaps someday, we’ll be able to measure their rotation directly.
Why black holes spin at nearly the speed of light
Black holes aren’t just the densest masses in the Universe, but they also spin the fastest of all massive objects. Here’s why it must be so.

Key Takeaways
- Black holes are some of the most enigmatic, extreme objects in the entire Universe, with more mass compressed into a tiny volume than any other object.
- But black holes aren’t just extremely massive, they’re also incredibly fast rotators. Many black holes, from their measured spins, are spinning at more than 90% the speed of light.
- This might seem like a puzzle, but physics not only has an explanation for why, but shows us that it’s very difficult to create black holes that spin slowly relative to the speed of light. Here’s why.
Share Why black holes spin at nearly the speed of light on Facebook
Share Why black holes spin at nearly the speed of light on Twitter
Share Why black holes spin at nearly the speed of light on LinkedIn
Whenever you take a look out there at the vast abyss of the deep Universe, it’s the points of light that stand out the most: stars and galaxies. While the majority of the light that you’ll first notice does indeed come from stars, a deeper look, going far beyond the visible portion of the electromagnetic spectrum, shows that there’s much more out there. The brightest, most massive stars, by their very nature, have the shortest lifespans, as they burn through their fuel far more quickly than their lower-mass counterparts. Once they’ve reached their limits and can fuse elements no further, they reach the end of their lives and become stellar corpses.
These corpses come in multiple varieties: white dwarfs for the lowest-mass (e.g., Sun-like) stars, neutron stars for the next tier up, and black holes for the most massive stars of all. These compact objects give off electromagnetic emissions spanning wavelengths from radio to X-ray light, revealing properties that range from mundane to absolutely shocking. While most stars themselves may spin relatively slowly, black holes rotate at nearly the speed of light. This might seem counterintuitive, but under the laws of physics, it couldn’t be any other way. Here’s why.

The closest analogue we have to one of those extreme objects in our own Solar System is the Sun. In another 7 billion years or so, after becoming a red giant and burning through the helium fuel that’s built up within its core, it will end its life by blowing off its outer layers while its core contracts down to a stellar remnant: the most gentle of all major types of stellar death.
The outer layers will create a sight known as a planetary nebula, which comes from the blown-off gases getting ionized and illuminated from the contracting central core. This nebula will glow for tens of thousands of years before cooling off and becoming neutral again, generally returning that material to the interstellar medium. When the opportunity then arises, those processed atoms will participate in future generations of star formation.
But the inner core, largely composed of carbon and oxygen, will contract down as far as it possibly can. In the end, gravitational collapse will only be stopped by the particles — atoms, ions, and electrons — that the remnant of our Sun will be made of.

So long as you remain below a critical mass threshold, the Chandrasekhar mass limit, the quantum properties inherent to those particles will be sufficient to hold the stellar remnant up against gravitational collapse. The endgame for a Sun-like star’s core will be a degenerate state known as a white dwarf. It will possess a sizable fraction of the mass of its parent star, but crammed into a tiny fraction of the volume: approximately the size of Earth.
Astronomers now know enough about stars and stellar evolution to describe what happens during this process. For a star like our Sun, approximately 60% of its mass will get expelled in the outer layers, while the remaining 40% remains in the core. The more massive a star becomes, the more mass, percentage-wise, gets blown off in its outer layers, with less being retained in the core. For the most massive stars that suffer the same fate as our Sun, possessing about 7-8 times the Sun’s mass, the mass fraction remaining in the core comes all the way down to about 18% of the original star’s mass.
This has happened nearby relatively recently, as the brightest star in Earth’s sky, Sirius, has a white dwarf companion, visible in the Hubble image below.

Sirius A is a little bit brighter and more massive than our Sun, and we believe that its binary companion, Sirius B, was once even more massive than Sirius A. Because the more massive stars burn through their nuclear fuel more quickly than lower-mass ones, Sirius B likely ran out of fuel some time ago. Today, Sirius A remains burning through its hydrogen fuel, and dominates that system in terms of mass and brightness. While Sirius A, today, weighs in at about twice the mass of our Sun, Sirius B is only approximately equal to our Sun’s mass.
However, based on observations of the white dwarfs that happen to pulse, we’ve learned a valuable lesson. Rather than taking multiple days or even (like our Sun) approximately a month to complete a full rotation, like normal stars tend to do, white dwarfs complete a full 360° rotation in as little as an hour. This might seem bizarre, but if you’ve ever seen a figure skating routine, the same principle that explains a spinning skater who pulls their arms in explains the white dwarfs rotational speed: the law of conservation of angular momentum.

Angular momentum is simply a measure of “How much rotational and/or orbital motion does a mass have to it?” If you puff that massive object up so that its mass is farther from its rotational center, it has to slow down in its rotational speed in order to conserve angular momentum. Similarly, if you compress a massive object down, so that more of its mass is closer to the center of its axis-of-rotation, it will have to speed up in its rotational speed, making more revolutions-per-second, to keep angular momentum conserved.
What happens, then, if you were to take a star like our Sun — with the mass, volume, and rotation speed of the Sun — and compressed it down into a volume the size of the Earth: a typical size for a white dwarf?
Believe it or not, if you make the assumption that angular momentum is conserved, and that both the Sun and the compressed version of the Sun we’re imagining are spheres, this is a completely solvable problem with only one possible answer. If we go conservative, and assume the entirety of the Sun rotates once every 33 days (the longest amount of time it takes any part of the Sun’s photosphere to complete one 360° rotation) and that only the inner 40% of the Sun becomes a white dwarf, you get a remarkable answer: the Sun, as a white dwarf, will complete a rotation in just 25 minutes.

By bringing all of that mass close in to the stellar remnant’s axis of rotation, we ensure that its rotational speed must rise. In general, if you halve the radius that an object has as it rotates, its rotational speed increases by a factor of four; rotational speed is inversely proportional to the square of a rotating mass’s radius. If you consider that it takes approximately 109 Earths to go across the diameter of the Sun, you can derive the same answer for yourself. (In reality, white dwarfs generally rotate a little more slowly, as the outermost layers get blown off, and only the interior “core” material contracts down to form a white dwarf.)
Unsurprisingly, then, you might start to ask about neutron stars or black holes: even more extreme objects. A neutron star is typically the product of a much more massive star ending its life in a supernova, where the particles in the core get so compressed that it behaves as one giant atomic nucleus composed almost exclusively (90% or more) of neutrons. Neutron stars are typically twice the mass of our Sun, but just about 10-to-40 km across. They rotate far more rapidly than any known star or white dwarf ever could.

Even the most naïve estimate you could make for the rotational speed of a neutron star — again, in analogy with our Sun — illustrates just how rapidly we can expect a neutron star to spin. If you repeated the thought experiment of compressing the entire Sun down into a smaller volume, but this time used one that was merely 40 kilometers in diameter, you’d get a much, much more rapid rotation rate than you ever could for a white dwarf: about 10 milliseconds. That same principle that we previously applied to a figure skater, about the conservation of angular momentum, leads us to the conclusion that neutron stars could complete more than 100 full rotations in a single second.
Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!
Fields marked with an * are required
In fact, this lines up perfectly with our actual observations. Some neutron stars emit radio pulses along Earth’s line-of-sight to them: pulsars. We can measure the pulse periods of these objects, and while some of them take approximately a full second to complete a rotation, some of them rotate in as little as 1.3 milliseconds, up to a maximum of 766 rotations-per-second.

The fastest-spinning neutron stars known are called millisecond pulsars, and they really do rotate at incredibly fast speeds. At their surfaces, those rotation rates are indeed relativistic: meaning they reach speeds that are a significant fraction of the speed of light. The most extreme examples of such neutron stars can reach speeds exceeding 50% the speed of light at the outer surface of these neutron stars.
But that doesn’t even approach the true astrophysical limits found in the Universe. Neutron stars aren’t the densest objects in the Universe; that honor goes to black holes, which take all the mass you’d find in a neutron star — more, in fact — and compress it down into a region of space where even an object moving at the speed of light couldn’t escape from it.
If you compressed the Sun down into a volume just 3 kilometers in radius, that would force it to become a black hole. And yet, the conservation of angular momentum would mean that much of that internal region would experience frame-dragging so severe that space itself would get dragged at speeds approaching the speed of light, even outside of the Schwarzschild radius of the black hole. The more you compress that mass down, the faster the fabric of space itself gets dragged.

Realistically, we can’t measure the frame-dragging of space itself in the vicinity of a black hole. But we can measure the frame-dragging effects on the matter that happens to be present within that space. For black holes, that means looking at the accretion disks and accretion flows found around these black holes that exist in matter-rich environments. Perhaps paradoxically, the smallest mass black holes, which have the smallest event horizons, actually have the largest amounts of spatial curvature at and near their event horizons.
You might think, therefore, that they’d make the best laboratories for testing these frame dragging effects. But nature surprised us on that front: a supermassive black hole at the center of galaxy NGC 1365 — which also happens to be one of the first galaxies imaged by the James Webb Space Telescope — has had the radiation emitted from the volume outside of it detected and measured, revealing its speed. Even at these large distances, the material spins at 84% the speed of light. If you insist that angular momentum be conserved, it couldn’t have turned out any other way.

Subsequently, we’ve inferred the spins of black holes that have merged together with gravitational wave observatories such as LIGO and Virgo, and found that some black holes spin at the theoretical maximum: around ~95% the speed of light. It’s a tremendously difficult thing to intuit: the notion that black holes should spin at almost the speed of light. After all, the stars that black holes are built from rotate extremely slowly, even by Earth’s standards of one rotation every 24 hours. Yet if you remember that most of the stars in our Universe also have enormous volumes, you’ll realize that they contain an enormous amount of angular momentum.
If you compress that volume down to be very small, those objects have no choice. If angular momentum has to be conserved, all they can do is spin up their rotational speeds until they almost reach the speed of light. At that point, gravitational waves will kick in, and some of that energy (and angular momentum) gets radiated away, bringing it back down to below the theoretical maximum value. If not for those processes, black holes might not be black after all, instead revealing naked singularities at their centers. In this Universe, black holes have no choice but to rotate at extraordinary speeds. Perhaps someday, we’ll be able to measure their rotation directly.
How the “Einstein shift” was predicted 8 years before General Relativity
The idea of gravitational redshift crossed Einstein’s mind years before General Relativity was complete. Here’s why it had to be there.

Key Takeaways
- One of the novel predictions that came along with Einstein’s novel theory of gravity was the idea of “the Einstein shift,” or as it’s known today, a gravitational redshift.
- But even though it wouldn’t be experimentally confirmed until a 1959 experiment, Einstein himself recognized it was an absolute necessity way back in 1907: a full 8 years before General Relativity was completed.
- Here’s the remarkable story of how, if you yourself had the same realizations that Einstein did more than 100 years ago, you could have predicted it too, even before General Relativity.
Share How the “Einstein shift” was predicted 8 years before General Relativity on Facebook
Share How the “Einstein shift” was predicted 8 years before General Relativity on Twitter
Share How the “Einstein shift” was predicted 8 years before General Relativity on LinkedIn
It’s extremely rare for any individual to bring about a scientific revolution through their work: where practically everyone conceived of the Universe in one way before that critical work was completed, and then afterward, our conception of the Universe was entirely different. In the case of Albert Einstein, this happened not just once, but multiple times. In 1905, Einstein brought us:
- the constancy of the speed of light,
- mass-energy equivalence (via E = mc²),
- and the special theory of relativity,
among other important advances. But arguably, Einstein’s biggest revolution came a decade later, in 1915, when he incorporated gravitation into relativity as well, leading to the general theory of relativity, or General Relativity, as it’s more commonly known.
With spacetime now understood as a dynamic entity, whose very fabric is curved by the presence and distribution of matter-and-energy, all sorts of new phenomena have been derived. Gravitational waves — ripples that travel through spacetime, carrying energy and moving at the speed of light — were predicted. The bending of starlight around massive, compact objects was an inevitable consequence, as were other gravitational effects like gravitational time dilation and additional orbital precessions.
But the first expected consequence ever predicted from General Relativity — the Einstein shift, also known as gravitational redshift — was predicted way back in 1907, by Einstein himself. Here’s not just how he did it, but how anyone with the same realization, including you, could have done it for themselves.

Imagine you have a photon — a single quantum of light — that’s propagating through space. Light isn’t just a quantum mechanical “energy packet,” but is also an electromagnetic wave. Each photon, or each electromagnetic wave, has a certain amount of energy inherent to it, and the precise amount of energy it possesses is related to its wavelength. Photons with shorter wavelengths have higher energies, with gamma rays, X-rays, and ultraviolet light all more energetic than visible light. Conversely, photons with longer wavelengths have lower amounts of energy inherent to them, with infrared, microwave, and radio waves all less energetic than visible light.
Now, we’ve known for a long time that other types of waves, like sound waves, will appear to be “shortened” or “lengthened” relative to the wavelength at which they were emitted dependent on the relative motions of the source and the observer. It’s the reason why an emergency vehicle’s siren (or an ice cream truck) sounds higher-pitched when it moves toward you, and then lower-pitched when it moves away from you: it’s an example of the Doppler shift.
And if light is a wave in precisely the same fashion, then the Doppler shift, once special relativity came along in 1905, must also apply to light.
Light can have its wavelength either stretched or compressed due to relative motion, in a Doppler redshift or a Doppler blueshift, but that’s hardly revolutionary or even unexpected. However, it was two years after special relativity, in 1907, that Einstein had what he’d later refer to as his happiest thought: the equivalence principle.
The equivalence principle, in its most straightforward form, simply states that there is nothing special or remarkable about gravitation at all; it’s simply another example of acceleration. If you were being accelerated, and you had no way of observing the source of your acceleration, could you tell the difference between whether propulsion, an external applied force, or a gravitational force was the cause of it.
With this realization — that gravitation was just another form of acceleration — Einstein recognized that it would be possible to make a more general theory of relativity that didn’t just incorporate all possible motions and changes in motions, but one that also included gravitation. Eight years later, his happiest thought would lead to General Relativity and a wholly new conception of how gravity worked.

But we wouldn’t have to wait until 1915 for the Einstein shift — what we now know as gravitational redshift (or gravitational blueshift) — to arise as a robust prediction. In fact, it was way back in 1907, when he first thought of the equivalence principle, that Einstein published his first prediction of this new type of redshift.
If you were in a spacecraft (or an elevator) that was accelerating upward, then a photon that was emitted from “beneath” you would have its wavelength stretched relative to its emitted wavelength by the time the photon caught up to your eyes. Similarly, if an identical photon were emitted from “above” you instead, its wavelength would appear compressed relative to the wavelength at which it was emitted. In the former case, you’d observe a Doppler redshift; in the latter, a Doppler blueshift.
By applying the equivalence principle, Einstein immediately recognized that the same shifts must apply if the acceleration were due to a gravitational field rather than a moving-and-accelerating spacecraft. If you’re seeing a photon rising up against a gravitational field, you’ll observe it to have a longer wavelength than when it was emitted, a gravitational redshift, and if you’re seeing a photon falling down into a gravitational field, you’ll observe that it has a shorter wavelength, or a gravitational blueshift.

Once Einstein developed both the equivalence principle and what would become his general theory of relativity more comprehensively, in 1911, he quantitatively was able to predict the gravitational redshift of a photon rising out of the gravitational field of the Sun: a prediction that wouldn’t be verified until 1962: seven years after his death. The only robust astronomical observation that ever confirmed gravitational redshift during Einstein’s lifetime came in 1954, when astronomer Daniel Popper measured a gravitational redshift for the spectral lines coming from the white dwarf 40 Eridani B, and found a strong agreement with the predictions of General Relativity.
There was a direct laboratory experiment in 1959, however, that provided our best confirmation of gravitational redshift: the Pound-Rebka experiment. By causing a particular isotope of iron to enter an excited nuclear state, that nucleus would then emit a gamma-ray photon of a specific wavelength. When sent upward, 22.5 meters, to an identical iron nucleus, the gravitational redshift changed that photon’s wavelength significantly enough that the higher nucleus couldn’t absorb it. Only if the nucleus was “driven” with an additional velocity — i.e., if it received an energetic “kick” — would there be enough extra energy in the photon that it would get absorbed again. When the calculation was performed to show how much energy must be added versus how much did General Relativity predict would be needed, the agreement was astounding: to within 1%.

Not everyone anticipated that this would be the case, however. Some thought that light wouldn’t respond to moving deeper into (or out of) a gravitational field by gaining (or losing) energy, as the equivalence principle demanded. After all, the equivalence principle’s main assertion was that objects that are accelerated by a gravitational force cannot be distinguished from objects that are accelerated by any other type of force: i.e., an inertial force. The tests we were able to perform of the equivalence principle, especially early on, only tested the equivalence of gravitational masses and inertial masses. Massless particles, like photons, had no such test for equivalence.
However, once the world knew about the existence of antimatter — which was indisputable by the early 1930s, both theoretically and experimentally — there was a simple thought experiment that one could have performed to show that it couldn’t be any other way. Matter and antimatter particles are the same in one way, as they have identical rest masses and, therefore (via E = mc²) identical rest mass energies. However, they have opposite electric charges (as well as other quantum numbers) from one another, and most spectacularly, if you collide a matter particle with its antimatter counterpart, they simply annihilate away into two photons of identical energy.

So, let’s imagine that this is precisely what we have: two particles, one matter and one antimatter. Only, instead of having them here on the surface of Earth, we have them high up above the Earth’s surface: with lots of gravitational potential energy. If we hold that particle-antiparticle pair at rest and simply allow them to annihilate with one another, then the energy of each of the two photons produced will be given by the rest mass energy inherent to each member of the particle-antiparticle pairs: E = mc². We’ll get two photons, and those photons will have well-defined energies.
But now, I’m going to set up two different scenarios for you, and you’re going to have to think about whether these two scenarios are permitted to have different outcomes or not.
- The particle-antiparticle pair annihilates up high in the gravitational field, producing two photons that eventually fall down, under the influence of gravity, to the surface of the Earth. Once there, we measure their combined energies.
- The particle-antiparticle pair are dropped from up high in the gravitational field, where they fall downward under the influence of gravity. Just before they hit the Earth’s surface, we allow them to annihilate, and then we measure their combined energies.
Let’s think about what’s happening in the second situation first. As the two masses fall in a gravitational field, they pick up speed, and therefore gain kinetic energy. When they’re just about to reach the surface of the Earth and they annihilate, they will produce two photons.
Now, what will the energy, combined, of those two photons be?
Because energy is conserved, both the rest mass energy and the kinetic energy of that particle-antiparticle pair must go into the energy of those two photons. The total energy of the two photons will be given by the sum of the rest mass energies and the kinetic energies of the particle and the antiparticle.
Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!
Fields marked with an * are required
It couldn’t be any other way, because energy must be conserved and there are no additional places for that energy to hide.

Now, let’s go back to the first situation: where the particle-antiparticle pair annihilates into two photons, and then the two photons fall deeper into the gravitational field until they reach the surface of the Earth.
Let’s once again consider, at the moment those two photons reach the surface of the Earth, what with their combined energy be?
Can you see, immediately, that a difference between these two situations isn’t allowed? If energy is conserved, then it cannot matter whether your matter antimatter pair:
- first annihilates into photons, and then those photons fall down deeper into a gravitational field, or
- falls down deeper into the gravitational field, and then that pair annihilates into photons.
If the starting conditions of both scenarios are identical, if there are no processes that occur in one scenario that don’t also occur in the other, and if the two photons wind up in the same (or equivalent) state at the end of both scenarios, then they must also have identical energies. The only way for that to be true is if photons, when they fall deeper into a gravitational field, experience the Einstein shift due to gravitation: in this case, a gravitational blueshift.
In many ways, this thought experiment illustrates perhaps the greatest difference between the older, Newtonian conception of gravitation and the modern one, General Relativity, given to us by Albert Einstein. In Newtonian gravity, it’s only an object’s rest mass that leads to gravitation. The force of gravity is determined by each of the two masses that are exerting the force on one another, as well as the distance (squared) between them. But in General Relativity, all forms of energy matter for gravitation, and all objects — even massless ones — are subject to gravity’s effects.
Since photons carry energy, a photon falling deeper into a gravitational field must gain energy, and a photon climbing out of a gravitational field must lose energy in order to escape. While massive particles would gain or lose speed, a photon cannot; it must always move at the universal speed for all massless particles, the speed of light. As a result, the only way photons can gain or lose energy is by changing their wavelength: blueshifting as they gain energy, redshifting as they lose it.
If energy is to be conserved, then photons must experience not just Doppler shifts due to the relative motion between an emitting source and the observer, but they’ll experience gravitational redshift and blueshifts — the Einstein shift — as well. Although it took approximately half-a-century to validate it observationally and experimentally, from a purely theoretical perspective, it never could have been any other way.
How the “Einstein shift” was predicted 8 years before General Relativity
The idea of gravitational redshift crossed Einstein’s mind years before General Relativity was complete. Here’s why it had to be there.

Key Takeaways
- One of the novel predictions that came along with Einstein’s novel theory of gravity was the idea of “the Einstein shift,” or as it’s known today, a gravitational redshift.
- But even though it wouldn’t be experimentally confirmed until a 1959 experiment, Einstein himself recognized it was an absolute necessity way back in 1907: a full 8 years before General Relativity was completed.
- Here’s the remarkable story of how, if you yourself had the same realizations that Einstein did more than 100 years ago, you could have predicted it too, even before General Relativity.
Share How the “Einstein shift” was predicted 8 years before General Relativity on Facebook
Share How the “Einstein shift” was predicted 8 years before General Relativity on Twitter
Share How the “Einstein shift” was predicted 8 years before General Relativity on LinkedIn
It’s extremely rare for any individual to bring about a scientific revolution through their work: where practically everyone conceived of the Universe in one way before that critical work was completed, and then afterward, our conception of the Universe was entirely different. In the case of Albert Einstein, this happened not just once, but multiple times. In 1905, Einstein brought us:
- the constancy of the speed of light,
- mass-energy equivalence (via E = mc²),
- and the special theory of relativity,
among other important advances. But arguably, Einstein’s biggest revolution came a decade later, in 1915, when he incorporated gravitation into relativity as well, leading to the general theory of relativity, or General Relativity, as it’s more commonly known.
With spacetime now understood as a dynamic entity, whose very fabric is curved by the presence and distribution of matter-and-energy, all sorts of new phenomena have been derived. Gravitational waves — ripples that travel through spacetime, carrying energy and moving at the speed of light — were predicted. The bending of starlight around massive, compact objects was an inevitable consequence, as were other gravitational effects like gravitational time dilation and additional orbital precessions.
But the first expected consequence ever predicted from General Relativity — the Einstein shift, also known as gravitational redshift — was predicted way back in 1907, by Einstein himself. Here’s not just how he did it, but how anyone with the same realization, including you, could have done it for themselves.

Imagine you have a photon — a single quantum of light — that’s propagating through space. Light isn’t just a quantum mechanical “energy packet,” but is also an electromagnetic wave. Each photon, or each electromagnetic wave, has a certain amount of energy inherent to it, and the precise amount of energy it possesses is related to its wavelength. Photons with shorter wavelengths have higher energies, with gamma rays, X-rays, and ultraviolet light all more energetic than visible light. Conversely, photons with longer wavelengths have lower amounts of energy inherent to them, with infrared, microwave, and radio waves all less energetic than visible light.
Now, we’ve known for a long time that other types of waves, like sound waves, will appear to be “shortened” or “lengthened” relative to the wavelength at which they were emitted dependent on the relative motions of the source and the observer. It’s the reason why an emergency vehicle’s siren (or an ice cream truck) sounds higher-pitched when it moves toward you, and then lower-pitched when it moves away from you: it’s an example of the Doppler shift.
And if light is a wave in precisely the same fashion, then the Doppler shift, once special relativity came along in 1905, must also apply to light.

Light can have its wavelength either stretched or compressed due to relative motion, in a Doppler redshift or a Doppler blueshift, but that’s hardly revolutionary or even unexpected. However, it was two years after special relativity, in 1907, that Einstein had what he’d later refer to as his happiest thought: the equivalence principle.
The equivalence principle, in its most straightforward form, simply states that there is nothing special or remarkable about gravitation at all; it’s simply another example of acceleration. If you were being accelerated, and you had no way of observing the source of your acceleration, could you tell the difference between whether propulsion, an external applied force, or a gravitational force was the cause of it.
With this realization — that gravitation was just another form of acceleration — Einstein recognized that it would be possible to make a more general theory of relativity that didn’t just incorporate all possible motions and changes in motions, but one that also included gravitation. Eight years later, his happiest thought would lead to General Relativity and a wholly new conception of how gravity worked.

But we wouldn’t have to wait until 1915 for the Einstein shift — what we now know as gravitational redshift (or gravitational blueshift) — to arise as a robust prediction. In fact, it was way back in 1907, when he first thought of the equivalence principle, that Einstein published his first prediction of this new type of redshift.
If you were in a spacecraft (or an elevator) that was accelerating upward, then a photon that was emitted from “beneath” you would have its wavelength stretched relative to its emitted wavelength by the time the photon caught up to your eyes. Similarly, if an identical photon were emitted from “above” you instead, its wavelength would appear compressed relative to the wavelength at which it was emitted. In the former case, you’d observe a Doppler redshift; in the latter, a Doppler blueshift.
By applying the equivalence principle, Einstein immediately recognized that the same shifts must apply if the acceleration were due to a gravitational field rather than a moving-and-accelerating spacecraft. If you’re seeing a photon rising up against a gravitational field, you’ll observe it to have a longer wavelength than when it was emitted, a gravitational redshift, and if you’re seeing a photon falling down into a gravitational field, you’ll observe that it has a shorter wavelength, or a gravitational blueshift.

Once Einstein developed both the equivalence principle and what would become his general theory of relativity more comprehensively, in 1911, he quantitatively was able to predict the gravitational redshift of a photon rising out of the gravitational field of the Sun: a prediction that wouldn’t be verified until 1962: seven years after his death. The only robust astronomical observation that ever confirmed gravitational redshift during Einstein’s lifetime came in 1954, when astronomer Daniel Popper measured a gravitational redshift for the spectral lines coming from the white dwarf 40 Eridani B, and found a strong agreement with the predictions of General Relativity.
There was a direct laboratory experiment in 1959, however, that provided our best confirmation of gravitational redshift: the Pound-Rebka experiment. By causing a particular isotope of iron to enter an excited nuclear state, that nucleus would then emit a gamma-ray photon of a specific wavelength. When sent upward, 22.5 meters, to an identical iron nucleus, the gravitational redshift changed that photon’s wavelength significantly enough that the higher nucleus couldn’t absorb it. Only if the nucleus was “driven” with an additional velocity — i.e., if it received an energetic “kick” — would there be enough extra energy in the photon that it would get absorbed again. When the calculation was performed to show how much energy must be added versus how much did General Relativity predict would be needed, the agreement was astounding: to within 1%.

Not everyone anticipated that this would be the case, however. Some thought that light wouldn’t respond to moving deeper into (or out of) a gravitational field by gaining (or losing) energy, as the equivalence principle demanded. After all, the equivalence principle’s main assertion was that objects that are accelerated by a gravitational force cannot be distinguished from objects that are accelerated by any other type of force: i.e., an inertial force. The tests we were able to perform of the equivalence principle, especially early on, only tested the equivalence of gravitational masses and inertial masses. Massless particles, like photons, had no such test for equivalence.
However, once the world knew about the existence of antimatter — which was indisputable by the early 1930s, both theoretically and experimentally — there was a simple thought experiment that one could have performed to show that it couldn’t be any other way. Matter and antimatter particles are the same in one way, as they have identical rest masses and, therefore (via E = mc²) identical rest mass energies. However, they have opposite electric charges (as well as other quantum numbers) from one another, and most spectacularly, if you collide a matter particle with its antimatter counterpart, they simply annihilate away into two photons of identical energy.

So, let’s imagine that this is precisely what we have: two particles, one matter and one antimatter. Only, instead of having them here on the surface of Earth, we have them high up above the Earth’s surface: with lots of gravitational potential energy. If we hold that particle-antiparticle pair at rest and simply allow them to annihilate with one another, then the energy of each of the two photons produced will be given by the rest mass energy inherent to each member of the particle-antiparticle pairs: E = mc². We’ll get two photons, and those photons will have well-defined energies.
But now, I’m going to set up two different scenarios for you, and you’re going to have to think about whether these two scenarios are permitted to have different outcomes or not.
- The particle-antiparticle pair annihilates up high in the gravitational field, producing two photons that eventually fall down, under the influence of gravity, to the surface of the Earth. Once there, we measure their combined energies.
- The particle-antiparticle pair are dropped from up high in the gravitational field, where they fall downward under the influence of gravity. Just before they hit the Earth’s surface, we allow them to annihilate, and then we measure their combined energies.

Let’s think about what’s happening in the second situation first. As the two masses fall in a gravitational field, they pick up speed, and therefore gain kinetic energy. When they’re just about to reach the surface of the Earth and they annihilate, they will produce two photons.
Now, what will the energy, combined, of those two photons be?
Because energy is conserved, both the rest mass energy and the kinetic energy of that particle-antiparticle pair must go into the energy of those two photons. The total energy of the two photons will be given by the sum of the rest mass energies and the kinetic energies of the particle and the antiparticle.
Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!
Fields marked with an * are required
It couldn’t be any other way, because energy must be conserved and there are no additional places for that energy to hide.

Now, let’s go back to the first situation: where the particle-antiparticle pair annihilates into two photons, and then the two photons fall deeper into the gravitational field until they reach the surface of the Earth.
Let’s once again consider, at the moment those two photons reach the surface of the Earth, what with their combined energy be?
Can you see, immediately, that a difference between these two situations isn’t allowed? If energy is conserved, then it cannot matter whether your matter antimatter pair:
- first annihilates into photons, and then those photons fall down deeper into a gravitational field, or
- falls down deeper into the gravitational field, and then that pair annihilates into photons.
If the starting conditions of both scenarios are identical, if there are no processes that occur in one scenario that don’t also occur in the other, and if the two photons wind up in the same (or equivalent) state at the end of both scenarios, then they must also have identical energies. The only way for that to be true is if photons, when they fall deeper into a gravitational field, experience the Einstein shift due to gravitation: in this case, a gravitational blueshift.

In many ways, this thought experiment illustrates perhaps the greatest difference between the older, Newtonian conception of gravitation and the modern one, General Relativity, given to us by Albert Einstein. In Newtonian gravity, it’s only an object’s rest mass that leads to gravitation. The force of gravity is determined by each of the two masses that are exerting the force on one another, as well as the distance (squared) between them. But in General Relativity, all forms of energy matter for gravitation, and all objects — even massless ones — are subject to gravity’s effects.
Since photons carry energy, a photon falling deeper into a gravitational field must gain energy, and a photon climbing out of a gravitational field must lose energy in order to escape. While massive particles would gain or lose speed, a photon cannot; it must always move at the universal speed for all massless particles, the speed of light. As a result, the only way photons can gain or lose energy is by changing their wavelength: blueshifting as they gain energy, redshifting as they lose it.
If energy is to be conserved, then photons must experience not just Doppler shifts due to the relative motion between an emitting source and the observer, but they’ll experience gravitational redshift and blueshifts — the Einstein shift — as well. Although it took approximately half-a-century to validate it observationally and experimentally, from a purely theoretical perspective, it never could have been any other way.
Not just light: Everything is a wave, including you
A concept known as “wave-particle duality” famously applies to light. But it also applies to all matter — including you.

Key Takeaways
- Quantum physics has redefined our understanding of matter.
- In the 1920s, the wave-particle duality of light was extended to include all material objects, from electrons to you.
- Cutting-edge experiments now explore how biological macromolecules can behave as both particle and wave.
Share Not just light: Everything is a wave, including you on Facebook
Share Not just light: Everything is a wave, including you on Twitter
Share Not just light: Everything is a wave, including you on LinkedIn
In 1905, the 26-year-old Albert Einstein proposed something quite outrageous: that light could be both wave or particle. This idea is just as weird as it sounds. How could something be two things that are so different? A particle is small and confined to a tiny space, while a wave is something that spreads out. Particles hit one another and scatter about. Waves refract and diffract. They add on or cancel each other out in superpositions. These are very different behaviors.
Hidden in translation
The problem with this wave-particle duality is that language has issues accommodating both behaviors coming from the same object. After all, language is built of our experiences and emotions, of the things we see and feel. We do not directly see or feel photons. We probe into their nature with experimental set-ups, collecting information through monitors, counters, and the like.
The photons’ dual behavior emerges as a response to how we set up our experiment. If we have light passing through narrow slits, it will diffract like a wave. If it collides with electrons, it will scatter like a particle. So, in a way, it is our experiment, the question we are asking, that determines the physical nature of light. This introduces a new element into physics: the observer’s interaction with the observed. In more extreme interpretations, we could almost say that the intention of the experimenter determines the physical nature of what is being observed — that the mind determines physical reality. That’s really out there, but what we can say for sure is that light responds to the question we are asking in different ways. In a sense, light is both wave and particle, and it is neither.
This brings us to Bohr’s model of the atom, which we discussed a couple of weeks back. His model pins electrons orbiting the atomic nucleus to specific orbits. The electron can only be in one of these orbits,as if it is set on a train track. It can jump between orbits, but it cannot be in between them. How does that work, exactly? To Bohr, it was an open question. The answer came from a remarkable feat of physical intuition, and it sparked a revolution in our understanding of the world.
The wave nature of a baseball
In 1924, Louis de Broglie, a historian turned physicist, showed quite spectacularly that the electron’s step-like orbits in Bohr’s atomic model are easily understood if the electron is pictured as consisting of standing waves surrounding the nucleus. These are waves much like the ones we see when we shake a rope that is attached at the other end. In the case of the rope, the standing wave pattern appears due to the constructive and destructive interference between waves going and coming back along the rope. For the electron, the standing waves appear for the same reason, but now the electron wave closes on itself like an ouroboros, the mythic serpent that swallows its own tail. When we shake our rope more vigorously, the pattern of standing waves displays more peaks. An electron at higher orbits corresponds to a standing wave with more peaks.
With Einstein’s enthusiastic support, de Broglie boldly extended the notion of wave-particle duality from light to electrons and, by extension, to every moving material object. Not only light, but matter of any kind was associated with waves.
De Broglie offered a formula known as de Broglie wavelength to compute the wavelength of any matter with mass m moving at velocity v. He associated wavelength λ to m and v — and thus to momentum p = mv — according to the relation λ = h/p, where h is Planck’s constant. The formula can be refined for objects moving close to the speed of light.
As an example, a baseball moving at 70 km per hour has an associated de Broglie wavelength of about 22 billionths of a trillionth of a trillionth of a centimeter (or 2.2 x 10-32 cm). Clearly, not much is waving there, and we are justified in picturing the baseball as a solid object. In contrast, an electron moving at one-tenth the speed of light has a wavelength about half the size of a hydrogen atom (more precisely, half the size of the most probable distance between an atomic nucleus and an electron at its lowest energy state).
Subscribe for counterintuitive, surprising, and impactful stories delivered to your inbox every Thursday
Fields marked with an * are required
While the wave nature of a moving baseball is irrelevant to understanding its behavior, the wave nature of the electron is essential to understand its behavior in atoms. The crucial point, though, is that everything waves. An electron, a baseball, and you.
Quantum biology
De Broglie’s remarkable idea has been confirmed in countless experiments. In college physics classes we demonstrate how electrons passing through a crystal diffract like waves, with superpositions creating dark and bright spots due to destructive and constructive interference. Anton Zeilinger, who shared the physics Nobel prize this year, has championed diffracting ever-larger objects, from the soccer-ball-shaped C60 molecule (with 60 carbon atoms) to biological macromolecules.
The question is how life under such a diffraction experiment would behave at the quantum level. Quantum biology is a new frontier, one where the wave-particle duality plays a key role in the behavior of living beings. Can life survive quantum superposition? Can quantum physics tell us something about the nature of life?
December 24th 2022
About Antimicrobial Resistance
Antimicrobial resistance happens when germs like bacteria and fungi develop the ability to defeat the drugs designed to kill them. That means the germs are not killed and continue to grow. Resistant infections can be difficult, and sometimes impossible, to treat.
Antimicrobial resistance is an urgent global public health threat, killing at least 1.27 million people worldwide and associated with nearly 5 million deaths in 2019. In the U.S., more than 2.8 million antimicrobial-resistant infections occur each year. More than 35,000 people die as a result, according to CDC’s 2019 Antibiotic Resistance (AR) Threats Report. When Clostridioides difficile—a bacterium that is not typically resistant but can cause deadly diarrhea and is associated with antimicrobial use—is added to these, the U.S. toll of all the threats in the report exceeds 3 million infections and 48,000 deaths.
December 21st 2022
Why 21 cm is the magic length for the Universe
Photons come in every wavelength you can imagine. But one particular quantum transition makes light at precisely 21 cm, and it’s magical.

Key Takeaways
- Across the observable Universe, there are some 10^80 atoms, and most of them are simple hydrogen: made of just one proton and one electron each.
- Every time a hydrogen atom forms, there’s a 50/50 shot that the proton and electron will have their spins aligned, which is a slightly higher-energy state than if they’re not aligned.
- The quantum transition from the aligned state to the anti-aligned state is one of the most extreme transitions of all, and it produces light of precisely 21 cm in wavelength: arguably the most important length in the Universe.
Share Why 21 cm is the magic length for the Universe on Facebook
Share Why 21 cm is the magic length for the Universe on Twitter
Share Why 21 cm is the magic length for the Universe on LinkedIn
In our Universe, quantum transitions are the governing rule behind every nuclear, atomic, and molecular phenomenon. Unlike the planets in our Solar System, which could stably orbit the Sun at any distance if they possessed the right speed, the protons, neutrons, and electrons that make up all the conventional matter we know of can only bind together in a specific set of configurations. These possibilities, although numerous, are finite in number, as the quantum rules that govern electromagnetism and the nuclear forces restrict how atomic nuclei and the electrons that orbit them can arrange themselves.
In all the Universe, the most common atom of all is hydrogen, with just one proton and one electron. Wherever new stars form, hydrogen atoms become ionized, becoming neutral again if those free electrons can find their way back to a free proton. Although the electrons will typically cascade down the allowed energy levels into the ground state, that normally produces only a specific set of infrared, visible, and ultraviolet light. But more importantly, a special transition occurs in hydrogen that produces light of about the size of your hand: 21 centimeters (about 8¼”) in wavelength. That’s a magic length, and it just might someday unlock the darkest secrets hiding out in the recesses of the Universe.

When it comes to the light in the Universe, wavelength is the one property that you can count on to reveal how that light was created. Even though light comes to us in the form of photons — individual quanta that, collectively, make up the phenomenon we know as light — there are two very different classes of quantum process that create the light that surrounds us: continuous ones and discrete ones.
A continuous process is something like the light emitted by the photosphere of the Sun. It’s a dark object that’s been heated up to a certain temperature, and it radiates light of all different, continuous wavelengths as dictated by that temperature: what physicists know as blackbody radiation.
A discrete process, however, doesn’t emit light of a continuous set of wavelengths, but rather only at extremely specific wavelengths. A good example of that is the light absorbed by the neutral atoms present within the extreme outer layers of the Sun. As the blackbody radiation strikes those neutral atoms, a few of those photons will have just the right wavelengths to be absorbed by the electrons within the neutral atoms they encounter. When we break sunlight up into its individual wavelengths, the various absorption lines present against the backdrop of continuous, blackbody radiation reveal both of these processes to us.

Each individual atom has its properties primarily defined by its nucleus, made up of protons (which determine its charge) and neutrons (which, combined with protons, determine its mass). Atoms also have electrons, which orbit the nucleus and occupy a specific set of energy levels. In isolation, each atom will come to exist in the ground state: where the electrons cascade down until they occupy the lowest allowable energy levels, limited only by the quantum rules that determine the various properties that electrons are and aren’t allowed to possess.
Electrons can occupy the ground state — the 1s orbital — of an atom until it’s full, which can hold two electrons. The next energy level up consists of spherical (the 2s) and perpendicular (the 2p) orbitals, which can hold two and six electrons, respectively, for a total of eight. The third energy level can hold 18 electrons: 3s (with two), 3p (with six), and 3d (with ten), and the pattern continues on upward. In general, the “upward” transitions rely on the absorption of a photon of particular wavelengths, while the “downward” transitions result in the emission of photons of the exact same wavelengths.

That’s the basic structure of an atom, sometimes referred to as “coarse structure.” When you transition from the third energy level to the second energy level in a hydrogen atom, for example, you produce a photon that’s red in color, with a wavelength of precisely 656.3 nanometers: right in the visible light range of human eyes.
But there are very, very slight differences between the exact, precise wavelength of a photon that gets emitted if you transition from:
- the third energy level down to either the 2s or the 2p orbital,
- an energy level where the spin angular momentum and the orbital angular momentum are aligned to one where they’re anti-aligned,
- or one where the nuclear spin and the electron spin are aligned versus anti-aligned.
There are rules as to what’s allowed versus what’s forbidden in quantum mechanics as well, such as the fact that you can transition an electron from a d-orbital to either an s-orbital or a p-orbital, and from an s-orbital to a p-orbital, but not from an s-orbital to another s-orbital.
The slight differences in energy between different types of orbital within the same energy level is known as an atom’s fine-structure, arising from the interaction between the spin of each particle within an atom and the orbital angular momentum of the electrons around the nucleus. It causes a shift in wavelength of less than 0.1%: small but measurable and significant.

But in quantum mechanics, even “forbidden” transitions can sometimes occur, owing to the phenomenon of quantum tunneling. Sure, you might not be able to transition from an s-orbital to another s-orbital directly, but if you can:
- transition from an s-orbital to a p-orbital and then back to an s-orbital,
- transition from an s-orbital to a d-orbital and then back to an s-orbital,
- or, more generally, transition from an s-orbital to any other allowable state and then back to an s-orbital,
then that transition can occur. The only thing weird about quantum tunneling is that you don’t have to have a “real” transition occur with enough energy to make it happen to the intermediate state; it can happen virtually, so that you only see the final state emerge from the initial state: something that would be forbidden without the invocation of quantum tunneling.
This allows us to go beyond mere “fine structure” and onto hyperfine structure, where the spin of the atomic nucleus and one of the electrons that orbit it begin in an “aligned” state, where the spins are both in the same direction even though the electron is in the lowest-energy, ground (1s) state, to an anti-aligned state, where the spins are reversed.
The most famous of these transitions occurs in the simplest type of atom of all: hydrogen. With just one proton and one electron, every time you form a neutral hydrogen atom and the electron cascades down to the ground (lowest-energy) state, there’s a 50% chance that the spins of the central proton and the electron will be aligned, with a 50% chance that the spins will be anti-aligned.
If the spins are anti-aligned, that’s truly the lowest-energy state; there’s nowhere to go via transition that will result in the emission of energy at all. But if the spins are aligned, it becomes possible to quantum tunnel to the anti-aligned state: even though the direct transition process is forbidden, tunneling allows you to go straight from the starting point to the ending point, emitting a photon in the process.
This transition, because of its “forbidden” nature, takes an extremely long time to occur: approximately 10 million years for the average atom. However, this long lifetime of the slightly excited, aligned case for a hydrogen atom has an upside to it: the photon that gets emitted, at 21 centimeters in wavelength and with a frequency of 1420 megahertz, is intrinsically, extremely narrow. In fact, it’s the narrowest, most precise transition line known in all of atomic and nuclear physics!
If you were to go all the way back to the early stages of the hot Big Bang, before any stars had formed, you’d discover that a whopping 92% of the atoms in the Universe were exactly this species of hydrogen: with one proton and one electron in them. As soon as neutral atoms stably form — just a few hundred thousand years after the Big Bang — these neutral hydrogen atoms form with a 50/50 chance of having aligned versus anti-aligned spins. The ones that form anti-aligned will remain so; the ones that form with their spins aligned will undergo this spin-flip transition, emitting radiation of 21 centimeters in wavelength.
Although it’s never yet been done, this gives us a tremendously provocative way to measure the early Universe: by finding a cloud of hydrogen-rich gas, even one that’s never formed stars, we could look for this spin-flip signal — accounting for the expansion of the Universe and the corresponding redshift of the light — to measure the atoms in the Universe from the earliest times ever seen. The only “broadening” to the line we’d expect to see would come from thermal and kinetic effects: from the non-zero temperature and the gravitationally-induced motion of the atoms that emit those 21 centimeter signals.

In addition to those primordial signals, 21 centimeter radiation arises as a consequence whenever new stars are produced. Every time that a star-forming event occurs, the more massive newborn stars produce large amounts of ultraviolet radiation: radiation that’s energetic enough to ionize hydrogen atoms. All of a sudden, space that was once filled with neutral hydrogen atoms is now filled with free protons and free electrons.
But those electrons are going to eventually be captured, once again, by those protons, and when there’s no longer enough ultraviolet radiation to ionize them over and over again, the electrons will once again sink down to the ground state, where they’ll have a 50/50 chance of being aligned or anti-aligned with the spin of the atomic nucleus.
Again, that same radiation — of 21 centimeters in wavelength — gets produced, and every time we measure that 21 centimeter wavelength localized in a specific region of space, even if it gets redshifted by the expansion of the Universe, what we’re seeing is evidence of recent star-formation. Wherever star-formation occurs, hydrogen gets ionized, and whenever those atoms become neutral and de-excite again, this specific-wavelength radiation persists for tens of millions of years.

If we had the capability of sensitively mapping this 21 centimeter emission in all directions and at all redshifts (i.e., distances) in space, we could literally uncover the star-formation history of the entire Universe, as well as the de-excitation of the hydrogen atoms first formed in the aftermath of the hot Big Bang. With sensitive enough observations, we could answer questions like:
Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!
Fields marked with an * are required
- Are there stars present in dark voids in space below the threshold of what we can observe, waiting to be revealed by their de-exciting hydrogen atoms?
- In galaxies where no new star-formation is observed, is star-formation truly over, or are there low-levels of new stars being born, just waiting to be discovered from this telltale signature of hydrogen atoms?
- Are there any events that heat up and lead to hydrogen ionization prior to the formation of the first stars, and are there star-formation bursts that exist beyond the capabilities of even our most powerful infrared observatories to observe directly?
By measuring light of precisely the needed wavelength — 21.106114053 centimeters, plus whatever lengthening effects arise from the cosmic expansion of the Universe — we could reveal the answers to all of these questions and more. In fact, this is one of the main science goals of LOFAR: the low-frequency array, and it presents a strong science case for putting an upscaled version of this array on the radio-shielded far side of the Moon.

Of course, there’s another possibility that takes us far beyond astronomy when it comes to making use of this important length: creating and measuring enough spin-aligned hydrogen atoms in the lab to detect this spin-flip transition directly, in a controlled fashion. The transition takes about ~10 million years to “flip” on average, which means we’d need around a quadrillion (1015) prepared atoms, kept still and cooled to cryogenic temperatures, to measure not only the emission line, but the width of it. If there are phenomena that cause an intrinsic line-broadening, such as a primordial gravitational wave signal, such an experiment would, quite remarkably, be able to uncover its existence and magnitude.
In all the Universe, there are only a few known quantum transitions with the precision inherent to the hyperfine spin-flip transition of hydrogen, resulting in the emission of radiation that’s 21 centimeters in wavelength. If we want to identify ongoing and recent star-formation across the Universe, the first atomic signals even before the first stars were formed, or the relic strength of yet-undetected gravitational waves left over from cosmic inflation, it becomes clear that the 21 centimeter transition is the most important probe we have in all the cosmos. In many ways, it’s the “magic length” for uncovering some of nature’s greatest secrets.
Tags
Did the Milky Way lose its black hole?
At four million solar masses, the Milky Way’s supermassive black hole is quite small for a galaxy its size. Did we lose the original?

Key Takeaways
- While many Milky Way-sized galaxies have supermassive black holes that are a hundred million solar masses or more, ours weighs in at just 4 million Suns.
- At the same time, we have some very good evidence that the Milky Way wasn’t a newcomer, but is more than 13 billion years old: almost as ancient as the Universe itself.
- Rather than being on the unlucky side, our supermassive black hole might be the second of its kind: only growing up after the original was ejected. It’s a wild idea, but science may yet validate it.
Share Did the Milky Way lose its black hole? on Facebook
Share Did the Milky Way lose its black hole? on Twitter
Share Did the Milky Way lose its black hole? on LinkedIn
At the heart of the Milky Way, a supermassive behemoth lurks. Formed over billions of years from a combination of merging black holes and the infalling matter that grows them, there now sits a mammoth black hole that weighs in at four million solar masses. It’s the largest black hole in the entire galaxy, and we’d have to travel millions of light-years away to find one that was more massive. From its perch in the galactic center, Sagittarius A* possesses the largest event horizon of any black hole we can observe from our current position in space.
And yet, despite how large, massive, and impressive this central black hole is, that’s only in comparison to the other black holes within our galaxy. When we look out at other large, massive galaxies — ones that are comparable to the Milky Way in size — we actually find that our supermassive black hole is on the rather small, low-mass side. While it’s possible that we’re simply a bit below average in the black hole department, there’s another potential explanation: perhaps the Milky Way once had a larger, truly supermassive black hole at its core, but it was ejected entirely a long time ago. What remains might be nothing more than an in-progress rebuilding project at the center of the Milky Way. Here’s the science of why we should seriously consider that our central, supermassive black hole might not be our galaxy’s original one.

When we take a look around at the galaxies in our vicinity, we find that they come in a wide variety of sizes, masses and shapes. As far as spiral galaxies go, the Milky Way is fairly typical of large, modern spirals, with an estimated 400 billion stars, a diameter that’s a little bit over 100,000 light-years, and populations of stars that date back more than 13 billion years: just shortly after the time of the Big Bang itself.
While the largest black holes of all, often exceeding billions or even tens of billions of solar masses are found overwhelmingly in the most massive galaxies we know of — giant elliptical galaxies — other comparable spirals generally have larger, more massive black holes than our own. For example:
- The Sombrero galaxy, about 30% of the Milky Way’s diameter, has a ~1 billion solar mass black hole.
- Andromeda, the closest large galaxy to the Milky Way and only somewhat larger, has a ~230 million solar mass black hole.
- NGC 5548, with an active nucleus but bright spiral arms, has a mass of around 70 million solar masses, comparable to that of nearby spirals Messier 81 and also Messier 58.
- And even Messier 82, much smaller and lower in mass than our own Milky Way (and interacting neighbor of Messier 81) has a black hole of 30 million solar masses.

In fact, of all of the spiral or elliptical galaxies known to host supermassive black holes, the Milky Way’s is the least massive one known. Additionally, only a few substantial galaxies have supermassive black holes that are even in the same ballpark as Sagittarius A* at the center of the Milky Way. A few spirals — all smaller than the Milky Way — such as Messier 61, NGC 7469, Messier 108 and NGC 3783, all have black holes between 5 and 30 million solar masses. These are some of the smallest supermassive black holes known, and while larger than ours, they’re at least comparable to the Milky Way’s 4.3 million central black hole.
Why would this be the case? There are really only two options.
- The first option is that there are many, many galaxies out there, and they have a huge range of black hole masses that they can obtain. We’re only seeing the ones that are easiest to see, and that’s going to be the most massive ones. There may be plenty of lower mass ones out there, and that’s the type we just happen to have.
- The second option, however, is that we’re actually well below the cosmic average in terms of the mass of our supermassive black hole, and there’s a physical reason — related to the evolution of our galaxy — that explains it.

We’re still learning, of course, how supermassive black holes form, grow, and evolve in the Universe. We’re still attempting to figure out all of the steps for how, when galaxies merge, their supermassive black holes can successfully inspiral and merge on short enough timescales to match what we observe. We’ve only recently just discovered the first object in the process of transitioning from a galaxy into a quasar, an important step in the evolution of supermassive black holes. And from observing the earliest galaxies and quasars of all, we find that these supermassive black holes can grow up remarkably fast: reaching masses of around ~1 billion solar masses in just the first 700 million years of cosmic evolution.
In theory, the story of how they form is straightforward.
- The earliest stars are very massive compared to the majority of stars that form today, and many of them will form black holes of tens, hundreds, or possibly even 1000 or more solar masses.
- These black holes won’t just feed on the gas, dust, and other matter that’s present, but will sink to the galaxy’s center and merge together on cosmically short timescales.
- As additional stars form, more and more matter gets “funneled” into the galactic center, growing these black holes further.
- And when intergalactic material accretes onto the galaxy — as well as when galaxies merge together — it typically results in a feeding frenzy for the black hole, growing its mass even more substantially.

Of course, we don’t know for certain how valid this story is. We have precious few high-quality observations of host galaxies and their black holes at those early epochs, and even those only give us a few specific snapshots. If the Hubble Space Telescope and the observatories of its era have shown us what the Universe looks like, it’s fair to say that the major science goal of the James Webb Space Telescope will be to teach us how the Universe grew up. In concert with large optical and infrared ground-based observatories, as well as giant radio arrays such as ALMA, we’ll have plenty of opportunities to either verify, refine, or overthrow our current picture of supermassive black hole formation and growth.
For our Milky Way, we have some pretty solid evidence that at least five significant galactic mergers occurred over the past ~11 billion years of our cosmic history: once the original, seed galaxy that our modern Milky Way would grow into was already firmly established. By that point in cosmic history, based upon how galaxies grow, we would expect to have a supermassive black hole that was at least in the tens-of-millions of solar masses range. With the passage of more time, we’d expect that the black hole would only have grown larger.
And yet today, some ~11 billion years later, our supermassive black hole is merely 4.3 million solar masses: less than 2% the mass of Andromeda’s supermassive black hole. It’s enough to make you wonder, “What is it, exactly, that happened (or didn’t happen) to us that resulted in our central black hole being so relatively small?”
It’s worth emphasizing that it is eminently possible that the Milky Way and our central black hole could simply be mundane. That perhaps nothing remarkable happened, and we’re simply able to make good enough observations from our close proximity to Sagittarius A* to determine its mass accurately. Perhaps many of these central black holes that we think are so massive might turn out to be smaller than we realize with our present technology.
But there’s a cosmic lesson that’s always worth remembering: at any moment, whenever we look out at an object in the Universe, we can only see the features whose evidence has survived until the present. This is true of our Solar System, which may have had more planets in the distant past, and it’s true of our galaxy, which may have had a much more massive central black hole a long time ago as well.
The Solar System, despite the tremendous difference in scale in comparison to the galaxy, is actually an excellent analogy. Now that we’ve discovered more than 5000 exoplanets, we know that our Solar System’s configuration — with all of the inner planets being small and rocky and all of the outer planets being large and gaseous — is not representative of what’s most common in the Universe. It’s likely that there was a fifth gas giant at one point, that it was ejected, and that the migration of the gas giants cleared out whatever early planets were present in the young Solar System.
Perhaps the reason we have Mercury, Venus, Earth, and Mars is because most of the material for forming planets was already used up in the inner part of the Solar System by the time their seeds came along, and this was as large as nature would let them get in the aftermath of that early “clearing out” event.
Well, it’s also plausible that the Milky Way formed a supermassive black hole the way that we believe most galaxies did, and that at some point we had a rather large one compared to what we see today. What could have happened? An event involving a large amount of gravitation — such as the merger of another galaxy or a strong enough “kick” from a nearby gravitational wave event — could have ejected it.

“Hold on,” you might object, “is there any evidence that supermassive black holes do get kicked out of galaxies?”
I’m glad you asked, because up until a decade ago, there wasn’t any. But back in 2012, astronomers were studying a system known as CID-42 in a galaxy some 4 billion light-years away. Previously, Hubble observations had revealed two distinct, compact sources that were observable in visible light: one at the center of the galaxy and one offset from the center.
Following up with NASA’s Chandra X-ray observatory, we found that there was a bright X-ray source consistent with heating from at least one supermassive black hole. Using the highest-resolution camera aboard Chandra, they found that the X-rays are only coming from one black hole, not two. But relative to one another, follow-up optical data showed that these two sources are moving away from one another at some 5 million kilometers-per-hour (~3 million miles-per-hour): well in excess of the escape velocity for a galaxy of that mass. As Dr. Francesa Civano, leader of the study, said back in 2012:
“It’s hard to believe that a supermassive black hole weighing millions of times the mass of the sun could be moved at all, let alone kicked out of a galaxy at enormous speed. But these new data support the idea that gravitational waves – ripples in the fabric of space first predicted by Albert Einstein but never detected directly – can exert an extremely powerful force.”
Recently, even though the science of gravitational wave astronomy is only about 5 years old at the time this article is being written, we got observational confirmation that such black hole “kicks” from gravitational waves aren’t particularly rare at all. Published on May 12, 2022, a study led by Dr. Vijay Varma showed that a black hole merger detected in 2020 — GW200129 — resulted in the most-merger black hole, owing to the relative properties of the progenitor black holes, receiving a tremendously fast “kick” of about 1500 km/s. For comparison, you only need to move at about one-third that speed to escape from the Milky Way’s gravitational pull.
Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!
Fields marked with an * are required
We’ve now seen fast-moving black holes of both the stellar mass and supermassive varieties. We’ve also seen how mergers can impart these kicks to black holes, particularly when gravitational waves are produced in predominantly one direction, which arises when the black holes have unequal masses or spins, and large precessions.
Putting these pieces together, it’s entirely reasonable that one of the Milky Way’s mergers over the past ~11 billion years resulted in the ejection of its initial central, supermassive black hole. What remains, today, may be merely the result of what it’s been able to regrow in the time that’s passed since.

It cannot be emphasized enough what a remarkable achievement it is that the Event Horizon Telescope collaboration has, at long last, finally imaged the supermassive black hole at the center of the Milky Way: Sagittarius A*. It confirmed, to better than 95% precision, at least one thing that we already knew from measuring the motions of the stars in the galactic center’s vicinity: that there’s an object their weighing in at an impressive 4.3 million solar masses. Nevertheless, as large as that value is, it’s extraordinarily down there on the low end for a supermassive black hole.
Did the Milky Way lose its black hole?
At four million solar masses, the Milky Way’s supermassive black hole is quite small for a galaxy its size. Did we lose the original?

Key Takeaways
- While many Milky Way-sized galaxies have supermassive black holes that are a hundred million solar masses or more, ours weighs in at just 4 million Suns.
- At the same time, we have some very good evidence that the Milky Way wasn’t a newcomer, but is more than 13 billion years old: almost as ancient as the Universe itself.
- Rather than being on the unlucky side, our supermassive black hole might be the second of its kind: only growing up after the original was ejected. It’s a wild idea, but science may yet validate it.
Share Did the Milky Way lose its black hole? on Facebook
Share Did the Milky Way lose its black hole? on Twitter
Share Did the Milky Way lose its black hole? on LinkedIn
At the heart of the Milky Way, a supermassive behemoth lurks. Formed over billions of years from a combination of merging black holes and the infalling matter that grows them, there now sits a mammoth black hole that weighs in at four million solar masses. It’s the largest black hole in the entire galaxy, and we’d have to travel millions of light-years away to find one that was more massive. From its perch in the galactic center, Sagittarius A* possesses the largest event horizon of any black hole we can observe from our current position in space.
And yet, despite how large, massive, and impressive this central black hole is, that’s only in comparison to the other black holes within our galaxy. When we look out at other large, massive galaxies — ones that are comparable to the Milky Way in size — we actually find that our supermassive black hole is on the rather small, low-mass side. While it’s possible that we’re simply a bit below average in the black hole department, there’s another potential explanation: perhaps the Milky Way once had a larger, truly supermassive black hole at its core, but it was ejected entirely a long time ago. What remains might be nothing more than an in-progress rebuilding project at the center of the Milky Way. Here’s the science of why we should seriously consider that our central, supermassive black hole might not be our galaxy’s original one.

When we take a look around at the galaxies in our vicinity, we find that they come in a wide variety of sizes, masses and shapes. As far as spiral galaxies go, the Milky Way is fairly typical of large, modern spirals, with an estimated 400 billion stars, a diameter that’s a little bit over 100,000 light-years, and populations of stars that date back more than 13 billion years: just shortly after the time of the Big Bang itself.
While the largest black holes of all, often exceeding billions or even tens of billions of solar masses are found overwhelmingly in the most massive galaxies we know of — giant elliptical galaxies — other comparable spirals generally have larger, more massive black holes than our own. For example:
- The Sombrero galaxy, about 30% of the Milky Way’s diameter, has a ~1 billion solar mass black hole.
- Andromeda, the closest large galaxy to the Milky Way and only somewhat larger, has a ~230 million solar mass black hole.
- NGC 5548, with an active nucleus but bright spiral arms, has a mass of around 70 million solar masses, comparable to that of nearby spirals Messier 81 and also Messier 58.
- And even Messier 82, much smaller and lower in mass than our own Milky Way (and interacting neighbor of Messier 81) has a black hole of 30 million solar masses.

In fact, of all of the spiral or elliptical galaxies known to host supermassive black holes, the Milky Way’s is the least massive one known. Additionally, only a few substantial galaxies have supermassive black holes that are even in the same ballpark as Sagittarius A* at the center of the Milky Way. A few spirals — all smaller than the Milky Way — such as Messier 61, NGC 7469, Messier 108 and NGC 3783, all have black holes between 5 and 30 million solar masses. These are some of the smallest supermassive black holes known, and while larger than ours, they’re at least comparable to the Milky Way’s 4.3 million central black hole.
Why would this be the case? There are really only two options.
- The first option is that there are many, many galaxies out there, and they have a huge range of black hole masses that they can obtain. We’re only seeing the ones that are easiest to see, and that’s going to be the most massive ones. There may be plenty of lower mass ones out there, and that’s the type we just happen to have.
- The second option, however, is that we’re actually well below the cosmic average in terms of the mass of our supermassive black hole, and there’s a physical reason — related to the evolution of our galaxy — that explains it.

We’re still learning, of course, how supermassive black holes form, grow, and evolve in the Universe. We’re still attempting to figure out all of the steps for how, when galaxies merge, their supermassive black holes can successfully inspiral and merge on short enough timescales to match what we observe. We’ve only recently just discovered the first object in the process of transitioning from a galaxy into a quasar, an important step in the evolution of supermassive black holes. And from observing the earliest galaxies and quasars of all, we find that these supermassive black holes can grow up remarkably fast: reaching masses of around ~1 billion solar masses in just the first 700 million years of cosmic evolution.
In theory, the story of how they form is straightforward.
- The earliest stars are very massive compared to the majority of stars that form today, and many of them will form black holes of tens, hundreds, or possibly even 1000 or more solar masses.
- These black holes won’t just feed on the gas, dust, and other matter that’s present, but will sink to the galaxy’s center and merge together on cosmically short timescales.
- As additional stars form, more and more matter gets “funneled” into the galactic center, growing these black holes further.
- And when intergalactic material accretes onto the galaxy — as well as when galaxies merge together — it typically results in a feeding frenzy for the black hole, growing its mass even more substantially.

Of course, we don’t know for certain how valid this story is. We have precious few high-quality observations of host galaxies and their black holes at those early epochs, and even those only give us a few specific snapshots. If the Hubble Space Telescope and the observatories of its era have shown us what the Universe looks like, it’s fair to say that the major science goal of the James Webb Space Telescope will be to teach us how the Universe grew up. In concert with large optical and infrared ground-based observatories, as well as giant radio arrays such as ALMA, we’ll have plenty of opportunities to either verify, refine, or overthrow our current picture of supermassive black hole formation and growth.
For our Milky Way, we have some pretty solid evidence that at least five significant galactic mergers occurred over the past ~11 billion years of our cosmic history: once the original, seed galaxy that our modern Milky Way would grow into was already firmly established. By that point in cosmic history, based upon how galaxies grow, we would expect to have a supermassive black hole that was at least in the tens-of-millions of solar masses range. With the passage of more time, we’d expect that the black hole would only have grown larger.

And yet today, some ~11 billion years later, our supermassive black hole is merely 4.3 million solar masses: less than 2% the mass of Andromeda’s supermassive black hole. It’s enough to make you wonder, “What is it, exactly, that happened (or didn’t happen) to us that resulted in our central black hole being so relatively small?”
It’s worth emphasizing that it is eminently possible that the Milky Way and our central black hole could simply be mundane. That perhaps nothing remarkable happened, and we’re simply able to make good enough observations from our close proximity to Sagittarius A* to determine its mass accurately. Perhaps many of these central black holes that we think are so massive might turn out to be smaller than we realize with our present technology.
But there’s a cosmic lesson that’s always worth remembering: at any moment, whenever we look out at an object in the Universe, we can only see the features whose evidence has survived until the present. This is true of our Solar System, which may have had more planets in the distant past, and it’s true of our galaxy, which may have had a much more massive central black hole a long time ago as well.
The Solar System, despite the tremendous difference in scale in comparison to the galaxy, is actually an excellent analogy. Now that we’ve discovered more than 5000 exoplanets, we know that our Solar System’s configuration — with all of the inner planets being small and rocky and all of the outer planets being large and gaseous — is not representative of what’s most common in the Universe. It’s likely that there was a fifth gas giant at one point, that it was ejected, and that the migration of the gas giants cleared out whatever early planets were present in the young Solar System.
Perhaps the reason we have Mercury, Venus, Earth, and Mars is because most of the material for forming planets was already used up in the inner part of the Solar System by the time their seeds came along, and this was as large as nature would let them get in the aftermath of that early “clearing out” event.
Well, it’s also plausible that the Milky Way formed a supermassive black hole the way that we believe most galaxies did, and that at some point we had a rather large one compared to what we see today. What could have happened? An event involving a large amount of gravitation — such as the merger of another galaxy or a strong enough “kick” from a nearby gravitational wave event — could have ejected it.

“Hold on,” you might object, “is there any evidence that supermassive black holes do get kicked out of galaxies?”
I’m glad you asked, because up until a decade ago, there wasn’t any. But back in 2012, astronomers were studying a system known as CID-42 in a galaxy some 4 billion light-years away. Previously, Hubble observations had revealed two distinct, compact sources that were observable in visible light: one at the center of the galaxy and one offset from the center.
Following up with NASA’s Chandra X-ray observatory, we found that there was a bright X-ray source consistent with heating from at least one supermassive black hole. Using the highest-resolution camera aboard Chandra, they found that the X-rays are only coming from one black hole, not two. But relative to one another, follow-up optical data showed that these two sources are moving away from one another at some 5 million kilometers-per-hour (~3 million miles-per-hour): well in excess of the escape velocity for a galaxy of that mass. As Dr. Francesa Civano, leader of the study, said back in 2012:
“It’s hard to believe that a supermassive black hole weighing millions of times the mass of the sun could be moved at all, let alone kicked out of a galaxy at enormous speed. But these new data support the idea that gravitational waves – ripples in the fabric of space first predicted by Albert Einstein but never detected directly – can exert an extremely powerful force.”

Recently, even though the science of gravitational wave astronomy is only about 5 years old at the time this article is being written, we got observational confirmation that such black hole “kicks” from gravitational waves aren’t particularly rare at all. Published on May 12, 2022, a study led by Dr. Vijay Varma showed that a black hole merger detected in 2020 — GW200129 — resulted in the most-merger black hole, owing to the relative properties of the progenitor black holes, receiving a tremendously fast “kick” of about 1500 km/s. For comparison, you only need to move at about one-third that speed to escape from the Milky Way’s gravitational pull.
Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!
Fields marked with an * are required
We’ve now seen fast-moving black holes of both the stellar mass and supermassive varieties. We’ve also seen how mergers can impart these kicks to black holes, particularly when gravitational waves are produced in predominantly one direction, which arises when the black holes have unequal masses or spins, and large precessions.
Putting these pieces together, it’s entirely reasonable that one of the Milky Way’s mergers over the past ~11 billion years resulted in the ejection of its initial central, supermassive black hole. What remains, today, may be merely the result of what it’s been able to regrow in the time that’s passed since.

It cannot be emphasized enough what a remarkable achievement it is that the Event Horizon Telescope collaboration has, at long last, finally imaged the supermassive black hole at the center of the Milky Way: Sagittarius A*. It confirmed, to better than 95% precision, at least one thing that we already knew from measuring the motions of the stars in the galactic center’s vicinity: that there’s an object their weighing in at an impressive 4.3 million solar masses. Nevertheless, as large as that value is, it’s extraordinarily down there on the low end for a supermassive black hole.
In all known galaxies of comparable size to the Milky Way, there is no other that has a supermassive black hole of such a low mass as our own. Although there’s still so much remaining to learn about black holes, including how they form, grow, and co-evolve with their host galaxies, one tantalizingly plausible explanation is that a major black hole ejection happened relatively late-in-the-game here in our home galaxy. Even though all we have left are the survivors, and the long-ago ejected behemoth may now be tens of millions of light-years away, it’s possible that this is one aspect of our cosmic history that may someday fall within our reach.
In all known galaxies of comparable size to the Milky Way, there is no other that has a supermassive black hole of such a low mass as our own. Although there’s still so much remaining to learn about black holes, including how they form, grow, and co-evolve with their host galaxies, one tantalizingly plausible explanation is that a major black hole ejection happened relatively late-in-the-game here in our home galaxy. Even though all we have left are the survivors, and the long-ago ejected behemoth may now be tens of millions of light-years away, it’s possible that this is one aspect of our cosmic history that may someday fall within our reach.

